Pencil (mathematics)

Last updated March 03, 2021

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.

Although the definition of a pencil is rather vague, the common characteristic is that the pencil is completely determined by any two of its members. Analogously, a set of geometric objects that are determined by any three of its members is called a bundle.^[1] Thus, the set of all lines through a point in three-space is a bundle of lines, any two of which determine a pencil of lines. To emphasize the two dimensional nature of such a pencil, it is sometimes referred to as a flat pencil^[2]

Any geometric object can be used in a pencil. The common ones are lines, planes, circles, conics, spheres and general curves. Even points can be used. A pencil of points is the set of all points on a given line.^[1] A more common term for this set is a range of points.

Pencil of lines

In a plane, let $u$ and $v$ be two distinct intersecting lines. For concreteness, suppose that $u$ has the equation, $aX + bY + c = 0$ and $v$ has the equation $a'X + b'Y + c' = 0$ . Then

λ u + μ v = 0

,

represents, for suitable scalars $λ$ and $μ$ , any line passing through the intersection of $u$ = 0 and $v$ = 0. This set of lines passing through a common point is called a pencil of lines.^[3] The common point of a pencil of lines is called the vertex of the pencil.

In an affine plane with the reflexive variant of parallelism, a set of parallel lines forms an equivalence class called a pencil of parallel lines.^[4] This terminology is consistent with the above definition since in the unique projective extension of the affine plane to a projective plane a single point (point at infinity) is added to each line in the pencil of parallel lines, thus making it a pencil in the above sense in the projective plane.

Pencil of planes

A pencil of planes, is the set of planes through a given straight line in three-space, called the axis of the pencil. The pencil is sometimes referred to as a axial-pencil^[5] or fan or a sheaf.^[6] For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.

Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.

In higher dimensional spaces, a pencil of hyperplanes consists of all the hyperplanes that contain a subspace of codimension 2. Such a pencil is determined by any two of its members.

Pencil of circles

Any two circles in the plane have a common radical axis, which is the line consisting of all the points that have the same power with respect to the two circles. A pencil of circles (or coaxial system) is the set of all circles in the plane with the same radical axis.^[7] To be inclusive, concentric circles are said to have the line at infinity as a radical axis.

There are five types of pencils of circles,^[8] the two families of Apollonian circles in the illustration above represent two of them. Each type is determined by two circles called the generators of the pencil. When described algebraically, it is possible that the equations may admit imaginary solutions. The types are:

An elliptic pencil (red family of circles in the figure) is defined by two generators that pass through each other in exactly two points. Every circle of an elliptic pencil passes through the same two points. An elliptic pencil does not include any imaginary circles.
A hyperbolic pencil (blue family of circles in the figure) is defined by two generators that do not intersect each other at any point. It includes real circles, imaginary circles, and two degenerate point circles called the Poncelet points of the pencil. Each point in the plane belongs to exactly one circle of the pencil.
A parabolic pencil (as a limiting case) is defined where two generating circles are tangent to each other at a single point. It consists of a family of real circles, all tangent to each other at a single common point. The degenerate circle with radius zero at that point also belongs to the pencil.
A family of concentric circles centered at a common center (may be considered a special case of a hyperbolic pencil where the other point is the point at infinity).
The family of straight lines through a common point; these should be interpreted as circles that all pass through the point at infinity (may be considered a special case of an elliptic pencil).^[9]^[10]

Properties

A circle that is orthogonal to two fixed circles is orthogonal to every circle in the pencil they determine.^[11]

The circles orthogonal to two fixed circles form a pencil of circles.^[11]

Two circles determine two pencils, the unique pencil that contains them and the pencil of circles orthogonal to them. The radical axis of one pencil consists of the centers of the circles of the other pencil. If one pencil is of elliptic type, the other is of hyperbolic type and vice versa.^[11]

The radical axis of any pencil of circles, interpreted as an infinite-radius circle, belongs to the pencil. Any three circles belong to a common pencil whenever all three pairs share the same radical axis and their centers are collinear.

Projective space of circles

There is a natural correspondence between circles in the plane and points in three-dimensional projective space; a line in this space corresponds to a one-dimensional continuous family of circles, hence a pencil of points in this space is a pencil of circles in the plane.

Specifically, the equation of a circle of radius $r$ centered at a point ( $p, q$ ),

(x-p)^{2}+(y-q)^{2}=r^{2},

may be rewritten as

\alpha (x^{2}+y^{2})-2\beta x-2\gamma y+\delta =0,

where $α = 1, β = p, γ = q, and δ = p 2 + q 2 - r 2$ . In this form, multiplying the quadruple ( $α,β,γ,δ$ ) by a scalar produces a different quadruple that represents the same circle; thus, these quadruples may be considered to be homogeneous coordinates for the space of circles.^[12] Straight lines may also be represented with an equation of this type in which $α = 0$ and should be thought of as being a degenerate form of a circle. When $α \neq 0$ , we may solve for $p = β/α, q = γ/α$ , and $r =\sqrt(p 2 + q 2 - δ/α)$ ; the latter formula may give $r = 0$ (in which case the circle degenerates to a point) or $r$ equal to an imaginary number (in which case the quadruple ( $α,β,γ,δ$ ) is said to represent an imaginary circle).

The set of affine combinations of two circles ( $α 1,β 1,γ 1,δ 1$ ), ( $α 2,β 2,γ 2,δ 2$ ), that is, the set of circles represented by the quadruple

z(\alpha _{1},\beta _{1},\gamma _{1},\delta _{1})+(1-z)(\alpha _{2},\beta _{2},\gamma _{2},\delta _{2})

for some value of the parameter $z$ , forms a pencil; the two circles being the generators of the pencil.

Cardioid as envelope of a pencil of circles

Another type of pencil of circles can be obtained as follows. Consider a given circle (called the generator circle) and a distinguished point $P$ on the generator circle. The set of all circles that pass through $P$ and have their centers on the generator circle form a pencil of circles. The envelope of this pencil is a cardioid.

Pencil of spheres

A sphere is uniquely determined by four points that are not coplanar. More generally, a sphere is uniquely determined by four conditions such as passing through a point, being tangent to a plane, etc.^[13] This property is analogous to the property that three non-collinear points determine a unique circle in a plane.

Consequently, a sphere is uniquely determined by (that is, passes through) a circle and a point not in the plane of that circle.

By examining the common solutions of the equations of two spheres, it can be seen that two spheres intersect in a circle and the plane containing that circle is called the radical plane of the intersecting spheres.^[14] Although the radical plane is a real plane, the circle may be imaginary (the spheres have no real point in common) or consist of a single point (the spheres are tangent at that point).^[15]

If $f (x, y, z) = 0$ and $g (x, y, z) = 0$ are the equations of two distinct spheres then

\lambda f(x,y,z)+\mu g(x,y,z)=0

is also the equation of a sphere for arbitrary values of the parameters $λ$ and $μ$ . The set of all spheres satisfying this equation is called a pencil of spheres determined by the original two spheres. In this definition a sphere is allowed to be a plane (infinite radius, center at infinity) and if both the original spheres are planes then all the spheres of the pencil are planes, otherwise there is only one plane (the radical plane) in the pencil.^[16]

If the pencil of spheres does not consist of all planes, then there are three types of pencils:^[15]

If the spheres intersect in a real circle $C$ , then the pencil consists of all the spheres containing $C$ , including the radical plane. The centers of all the ordinary spheres in the pencil lie on a line passing through the center of $C$ and perpendicular to the radical plane.
If the spheres intersect in an imaginary circle, all the spheres of the pencil also pass through this imaginary circle but as ordinary spheres they are disjoint (have no real points in common). The line of centers is perpendicular to the radical plane, which is a real plane in the pencil containing the imaginary circle.
If the spheres intersect in a point $A$ , all the spheres in the pencil are tangent at $A$ and the radical plane is the common tangent plane of all these spheres. The line of centers is perpendicular to the radical plane at $A$ .

All the tangent lines from a fixed point of the radical plane to the spheres of a pencil have the same length.^[15]

The radical plane is the locus of the centers of all the spheres that are orthogonal to all the spheres in a pencil. Moreover, a sphere orthogonal to any two spheres of a pencil of spheres is orthogonal to all of them and its center lies in the radical plane of the pencil.^[15]

Pencil of conics

A (non-degenerate) conic is completely determined by five points in general position (no three collinear) in a plane and the system of conics which pass through a fixed set of four points (again in a plane and no three collinear) is called a pencil of conics.^[17] The four common points are called the base points of the pencil. Through any point other than a base point, there passes a single conic of the pencil. This concept generalizes a pencil of circles.

In a projective plane defined over an algebraically closed field any two conics meet in four points (counted with multiplicity) and so, determine the pencil of conics based on these four points. Furthermore, the four base points determine three line pairs (degenerate conics through the base points, each line of the pair containing exactly two base points) and so each pencil of conics will contain at most three degenerate conics.^[18]

A pencil of conics can be represented algebraically in the following way. Let $C 1$ and $C 2$ be two distinct conics in a projective plane defined over an algebraically closed field $K$ . For every pair $λ, μ$ of elements of $K$ , not both zero, the expression:

\lambda C_{1}+\mu C_{2}

represents a conic in the pencil determined by $C 1$ and $C 2$ . This symbolic representation can be made concrete with a slight abuse of notation (using the same notation to denote the object as well as the equation defining the object.) Thinking of $C 1$ , say, as a ternary quadratic form, then $C 1 = 0$ is the equation of the "conic $C 1$ ". Another concrete realization would be obtained by thinking of $C 1$ as the 3×3 symmetric matrix which represents it. If $C 1$ and $C 2$ have such concrete realizations then every member of the above pencil will as well. Since the setting uses homogeneous coordinates in a projective plane, two concrete representations (either equations or matrices) give the same conic if they differ by a non-zero multiplicative constant.

Pencil of plane curves

More generally, a pencil is the special case of a linear system of divisors in which the parameter space is a projective line. Typical pencils of curves in the projective plane, for example, are written as

\lambda C+\mu C'=0\,

where $C = 0$ , $C' = 0$ are plane curves.

History

Desargues is credited with inventing the term "pencil of lines" (ordonnance de lignes).^[19]

An early author of modern projective geometry G. B. Halsted introduced many terms, most of which are now considered to be archaic.^{[ according to whom? ]} For example, "Straights with the same cross are copunctal." Also "The aggregate of all coplanar, copunctal straights is called a flat-pencil" and "A piece of a flat-pencil bounded by two of the straights as sides, is called an angle."^[20]

Notes

1 2 Young 1971 , p. 40
↑ Halsted 1906 , p. 9
↑ Pedoe 1988 , p. 106
↑ Artin 1957 , p. 53
↑ Halsted 1906 , p. 9
↑ Woods 1961 , p. 12
↑ Johnson 2007 , p. 34
↑ Some authors combine types and reduce the list to three. Schwerdtfeger (1979 , pp. 8–10)
↑ Johnson 2007 , p. 36
↑ Schwerdtfeger 1979 , pp. 8–10
1 2 3 Johnson 2007 , p. 37
↑ Pfeifer & Van Hook 1993.
↑ Albert 2016 , p. 55.
↑ Albert 2016 , p. 57.
1 2 3 4 Woods 1961 , p. 267.
↑ Woods 1961 , p. 266
↑ Faulkner 1952 , pg. 64.
↑ Samuel 1988 , pg. 50.
↑ Earliest Known Uses of Some Words of Mathematics , retrieved July 14, 2020
↑ Halsted 1906 , p. 9

Related Research Articles

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

A sphere is a geometrical object in three-dimensional space that is the surface of a ball.

In mathematics, the matrix representation of conic sections permits the tools of linear algebra to be used in the study of conic sections. It provides easy ways to calculate a conic section's axis, vertices, tangents and the pole and polar relationship between points and lines of the plane determined by the conic. The technique does not require putting the equation of a conic section into a standard form, thus making it easier to investigate those conic sections whose axes are not parallel to the coordinate system.

In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied.

A vanishing point is a point on the image plane of a perspective drawing where the two-dimensional perspective projections of mutually parallel lines in three-dimensional space appear to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the oculus, or "eye point", from which the image should be viewed for correct perspective geometry. Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points.

In geometry, the radical axis of two non-concentric circles is a line defined from the two circles, perpendicular to the line connecting the centers of the circles. If the circles cross, their radical axis is the line through their two crossing points, and if they are tangent, it is their line of tangency. For two disjoint circles, the radical axis is the locus of points at which tangents drawn to both circles have equal lengths.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.

The circles of Apollonius are any of several sets of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a sphere can be defined through stereographic projection.

Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greek geometer.

In triangle geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

In algebraic geometry, the conic sections in the projective plane form a linear system of dimension five, as one sees by counting the constants in the degree two equations. The condition to pass through a given point P imposes a single linear condition, so that conics C through P form a linear system of dimension 4. Other types of condition that are of interest include tangency to a given line L.

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines should be regarded as circles of infinite radius and that points in the plane should be regarded as circles of zero radius.

In inversive geometry, the circle of antisimilitude of two circles, α and β, is a reference circle for which α and β are inverses of each other. If α and β are non-intersecting or tangent, a single circle of antisimilitude exists; if α and β intersect at two points, there are two circles of antisimilitude. When α and β are congruent, the circle of antisimilitude degenerates to a line of symmetry through which α and β are reflections of each other.

In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles, where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (n^th) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.

Conic section Curve obtained by intersecting a cone and a plane

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.

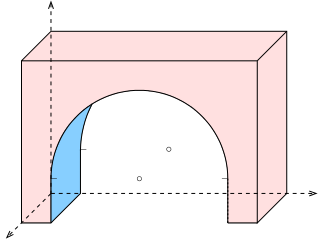
Axonometry is a graphical procedure belonging to descriptive geometry that generates a planar image of a three-dimensional object. The term "axonometry" means "to measure along axes", and indicates that the dimensions and scaling of the coordinate axes play a crucial role. The result of an axonometric procedure is a uniformly-scaled parallel projection of the object. In general, the resulting parallel projection is oblique ; but in special cases the result is orthographic, which in this context is called an orthogonal axonometry.

In differential geometry Dupin's theorem, named after the French mathematician Charles Dupin, is the statement:

References

Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
Artin, E. (1957), Geometric Algebra, Interscience Publishers
Faulkner, T. E. (1952), Projective Geometry (2nd ed.), Edinburgh: Oliver and Boyd
Halsted, George Bruce (1906). Synthetic Projective Geometry.
Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
Pedoe, Dan (1988) [1970], Geometry /A Comprehensive Course, Dover, ISBN 0-486-65812-0
Pfeifer, Richard E.; Van Hook, Cathleen (1993), "Circles, Vectors, and Linear Algebra", Mathematics Magazine, 66 (2): 75–86, doi:10.2307/2691113, JSTOR 2691113
Samuel, Pierre (1988), Projective Geometry , Undergraduate Texts in Mathematics (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4
Schwerdtfeger, Hans (1979) [1962], Geometry of Complex Numbers: Circle Geometry, Moebius Transformation, Non-Euclidean Geometry, Dover, pp. 8–10.
Young, John Wesley (1971) [1930], Projective Geometry, Carus Monograph #4, Mathematical Association of America
Woods, Frederick S. (1961) [1922], Higher Geometry / An introduction to advanced methods in analytic geometry, Dover

External links

Weisstein, Eric W. "Pencil". MathWorld .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Young40-1] 1 2 Young 1971 , p. 40

[2] Halsted 1906 , p. 9

[3] Pedoe 1988 , p. 106

[4] Artin 1957 , p. 53

[5] Halsted 1906 , p. 9

[6] Woods 1961 , p. 12

[7] Johnson 2007 , p. 34

[8] Some authors combine types and reduce the list to three. Schwerdtfeger (1979 , pp. 8–10)

[9] Johnson 2007 , p. 36

[10] Schwerdtfeger 1979 , pp. 8–10

[Jo37-11] 1 2 3 Johnson 2007 , p. 37

[12] Pfeifer & Van Hook 1993.

[13] Albert 2016 , p. 55.

[14] Albert 2016 , p. 57.

[Woods267-15] 1 2 3 4 Woods 1961 , p. 267.

[Woods266-16] Woods 1961 , p. 266

[17] Faulkner 1952 , pg. 64.

[18] Samuel 1988 , pg. 50.

[19] Earliest Known Uses of Some Words of Mathematics , retrieved July 14, 2020

[20] Halsted 1906 , p. 9

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]