Five points determine a conic

In Euclidean and projective geometry, five points determine a conic (a degree-2 plane curve), just as two (distinct) points determine a line (a degree-1 plane curve). There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.

Formally, given any five points in the plane in general linear position, meaning no three collinear, there is a unique conic passing through them, which will be non-degenerate; this is true over both the Euclidean plane and any pappian projective plane. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate (reducible, because it contains a line), and may not be unique; see further discussion.

Proofs

This result can be proven numerous different ways; the dimension counting argument is most direct, and generalizes to higher degree, while other proofs are special to conics.

Dimension counting

Intuitively, passing through five points in general linear position specifies five independent linear constraints on the (projective) linear space of conics, and hence specifies a unique conic, though this brief statement ignores subtleties.

More precisely, this is seen as follows:

• conics correspond to points in the five-dimensional projective space ${\displaystyle \mathbf {P} ^{5};}$
• requiring a conic to pass through a point imposes a linear condition on the coordinates: for a fixed ${\displaystyle (x,y),}$ the equation ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}$ is a linear equation in ${\displaystyle (A,B,C,D,E,F);}$
• by dimension counting, five constraints (that the curve passes through five points) are necessary to specify a conic, as each constraint cuts the dimension of possibilities by 1, and one starts with 5 dimensions;
• in 5 dimensions, the intersection of 5 (independent) hyperplanes is a single point (formally, by Bézout's theorem);
• general linear position of the points means that the constraints are independent, and thus do specify a unique conic;
• the resulting conic is non-degenerate because it is a curve (since it has more than 1 point), and does not contain a line (else it would split as two lines, at least one of which must contain 3 of the 5 points, by the pigeonhole principle), so it is irreducible.

The two subtleties in the above analysis are that the resulting point is a quadratic equation (not a linear equation), and that the constraints are independent. The first is simple: if A, B, and C all vanish, then the equation ${\displaystyle Dx+Ey+F=0}$ defines a line, and any 3 points on this (indeed any number of points) lie on a line – thus general linear position ensures a conic. The second, that the constraints are independent, is significantly subtler: it corresponds to the fact that given five points in general linear position in the plane, their images in ${\displaystyle \mathbf {P} ^{5}}$ under the Veronese map are in general linear position, which is true because the Veronese map is biregular: i.e., if the image of five points satisfy a relation, then the relation can be pulled back and the original points must also satisfy a relation. The Veronese map has coordinates ${\displaystyle [x^{2}:xy:y^{2}:xz:yz:z^{2}],}$ and the target ${\displaystyle \mathbf {P} ^{5}}$ is dual to the ${\displaystyle [A:B:C:D:E:F]}$${\displaystyle \mathbf {P} ^{5}}$ of conics. The Veronese map corresponds to "evaluation of a conic at a point", and the statement about independence of constraints is exactly a geometric statement about this map.

Synthetic proof

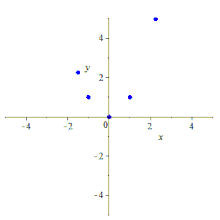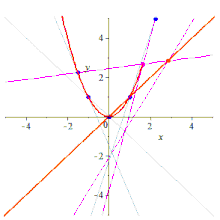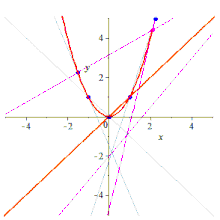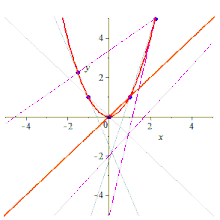
That five points determine a conic can be proven by synthetic geometry —i.e., in terms of lines and points in the plane—in addition to the analytic (algebraic) proof given above. Such a proof can be given using a theorem of Jakob Steiner, ^[1] which states:

Given a projective transformation f, between the pencil of lines passing through a point X and the pencil of lines passing through a point Y, the set C of intersection points between a line x and its image ${\displaystyle f(x)}$ forms a conic.

Note that X and Y are on this conic by considering the preimage and image of the line XY (which is respectively a line through X and a line through Y).

This can be shown by taking the points X and Y to the standard points ${\displaystyle [1:0:0]}$ and ${\displaystyle [0:1:0]}$ by a projective transformation, in which case the pencils of lines correspond to the horizontal and vertical lines in the plane, and the intersections of corresponding lines to the graph of a function, which (must be shown) is a hyperbola, hence a conic, hence the original curve C is a conic.

Now given five points X, Y, A, B, C, the three lines ${\displaystyle XA,XB,XC}$ can be taken to the three lines ${\displaystyle YA,YB,YC}$ by a unique projective transform, since projective transforms are simply 3-transitive on lines (they are simply 3-transitive on points, hence by projective duality they are 3-transitive on lines). Under this map X maps to Y, since these are the unique intersection points of these lines, and thus satisfy the hypothesis of Steiner’s theorem. The resulting conic thus contains all five points, and is the unique such conic, as desired.

Parabola construction, given five points

Construction

Given five points, one can construct the conic containing them in various ways.

Analytically, given the coordinates ${\displaystyle (x_{i},y_{i})_{i=1,2,3,4,5}}$ of the five points, the equation for the conic can be found by linear algebra, by writing and solving the five equations in the coefficients, substituting the variables with the values of the coordinates: five equations, six unknowns, but homogeneous so scaling removes one dimension; concretely, setting one of the coefficients to 1 accomplishes this.

This can be achieved quite directly as the following determinantal equation:

${\displaystyle \det {\begin{bmatrix}x^{2}&xy&y^{2}&x&y&1\\x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}&x_{3}y_{3}&y_{3}^{2}&x_{3}&y_{3}&1\\x_{4}^{2}&x_{4}y_{4}&y_{4}^{2}&x_{4}&y_{4}&1\\x_{5}^{2}&x_{5}y_{5}&y_{5}^{2}&x_{5}&y_{5}&1\end{bmatrix}}=0}$

This matrix has variables in its first row and numbers in all other rows, so the determinant is visibly a linear combination of the six monomials of degree at most 2. Also, the resulting polynomial clearly vanishes at the five input points (when ${\displaystyle (x,y)=(x_{i},y_{i})}$), as the matrix has then a repeated row.

Synthetically, the conic can be constructed by the Braikenridge–Maclaurin construction, ^{[2] [3] [4] [5]} by applying the Braikenridge–Maclaurin theorem, which is the converse of Pascal's theorem. Pascal's theorem states that given 6 points on a conic (a hexagon), the lines defined by opposite sides intersect in three collinear points. This can be reversed to construct the possible locations for a 6th point, given 5 existing ones.

Generalizations

The natural generalization is to ask for what value of k a configuration of k points (in general position) in n-space determines a variety of degree d and dimension m, which is a fundamental question in enumerative geometry.

A simple case of this is for a hypersurface (a codimension 1 subvariety, the zeros of a single polynomial, the case ${\displaystyle m=n-1}$), of which plane curves are an example.

In the case of a hypersurface, the answer is given in terms of the multiset coefficient, more familiarly the binomial coefficient, or more elegantly the rising factorial, as:

${\displaystyle k=\left(\!\!{n+1 \choose d}\!\!\right)-1={n+d \choose d}-1={\frac {1}{n!}}(d+1)^{(n)}-1.}$

This is via the analogous analysis of the Veronese map: k points in general position impose k independent linear conditions on a variety (because the Veronese map is biregular), and the number of monomials of degree d in ${\displaystyle n+1}$ variables (n-dimensional projective space has ${\displaystyle n+1}$ homogeneous coordinates) is ${\displaystyle \textstyle {\left(\!\!{n+1 \choose d}\!\!\right)},}$ from which 1 is subtracted because of projectivization: multiplying a polynomial by a constant does not change its zeros.

In the above formula, the number of points k is a polynomial in d of degree n, with leading coefficient ${\displaystyle 1/n!}$

In the case of plane curves, where ${\displaystyle n=2,}$ the formula becomes:

${\displaystyle \textstyle {\frac {1}{2}}(d+1)(d+2)-1=\textstyle {\frac {1}{2}}(d^{2}+3d)}$

whose values for ${\displaystyle d=0,1,2,3,4}$ are ${\displaystyle 0,2,5,9,14}$ – there are no curves of degree 0 (a single point is a point and is thus determined by a point, which is codimension 2), 2 points determine a line, 5 points determine a conic, 9 points determine a cubic, 14 points determine a quartic, and so forth.

Related results

While five points determine a conic, sets of six or more points on a conic are not in general position, that is, they are constrained as is demonstrated in Pascal's theorem.

Similarly, while nine points determine a cubic, if the nine points lie on more than one cubic—i.e., they are the intersection of two cubics—then they are not in general position, and indeed satisfy an addition constraint, as stated in the Cayley–Bacharach theorem.

Four points do not determine a conic, but rather a pencil, the 1-dimensional linear system of conics which all pass through the four points (formally, have the four points as base locus). Similarly, three points determine a 2-dimensional linear system (net), two points determine a 3-dimensional linear system (web), one point determines a 4-dimensional linear system, and zero points place no constraints on the 5-dimensional linear system of all conics.

The Apollonian circles are two 1-parameter families determined by 2 points.

As is well known, three non-collinear points determine a circle in Euclidean geometry and two distinct points determine a pencil of circles such as the Apollonian circles. These results seem to run counter the general result since circles are special cases of conics. However, in a pappian projective plane a conic is a circle only if it passes through two specific points on the line at infinity, so a circle is determined by five non-collinear points, three in the affine plane and these two special points. Similar considerations explain the smaller than expected number of points needed to define pencils of circles.

Tangency

Instead of passing through points, a different condition on a curve is being tangent to a given line. Being tangent to five given lines also determines a conic, by projective duality, but from the algebraic point of view tangency to a line is a quadratic constraint, so naive dimension counting yields 2⁵ = 32 conics tangent to five given lines, of which 31 must be ascribed to degenerate conics, as described in fudge factors in enumerative geometry; formalizing this intuition requires significant further development to justify.

Another classic problem in enumerative geometry, of similar vintage to conics, is the Problem of Apollonius: a circle that is tangent to three circles in general determines eight circles, as each of these is a quadratic condition and 2³ = 8. As a question in real geometry, a full analysis involves many special cases, and the actual number of circles may be any number between 0 and 8, except for 7.

See also

• Cramer's theorem (algebraic curves), for a generalization to n-th degree planar curves

References

1. Interactive Course on Projective Geometry Archived 2017-11-27 at the Wayback Machine , Chapter Five: The Projective Geometry of Conics Archived 2017-12-22 at the Wayback Machine : Section Four: Conics on the real projective plane Archived 2018-04-24 at the Wayback Machine , by J.C. Álvarez Paiva; proof follows Exercise 4.6
2. ( Coxeter 1961 , pp. 252–254)
3. The Animated Pascal, Sandra Lach Arlinghaus
4. Weisstein, Eric W. "Braikenridge-Maclaurin Construction." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Braikenridge-MaclaurinConstruction.html
5. The GNU 3DLDF Conic Sections Page: Pascal's Theorem and the Braikenridge-Maclaurin Construction, Laurence D. Finston

• Coxeter, H. S. M. (1961), Introduction to Geometry, Washington, DC
• Coxeter, H. S. M.; Greitzer, S. L. (1967), Geometry Revisited, Washington, DC: Mathematical Association of America, p. 76
• Dixon, A. C. (March 1908), "The Conic through Five Given Points", The Mathematical Gazette, The Mathematical Association, 4 (70): 228–230, doi:10.2307/3605147, JSTOR   3605147

External links

• Five Points Determine a Conic Section, Wolfram interactive demonstration