
Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in n-dimensional Euclidean space.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the distances from the isodynamic point to the triangle vertices are inversely proportional to the opposite side lengths of the triangle. Triangles that are similar to each other have isodynamic points in corresponding locations in the plane, so the isodynamic points are triangle centers, and unlike other triangle centers the isodynamic points are also invariant under Möbius transformations. A triangle that is itself equilateral has a unique isodynamic point, at its centroid(as well as its orthocenter, its incenter, and its circumcenter, which are concurrent); every non-equilateral triangle has two isodynamic points. Isodynamic points were first studied and named by Joseph Neuberg (1885).

In geometry, the Nagel point is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. It is the point of concurrency of all three of the triangle's splitters.

In geometry, a triangle center or triangle centre is a point in the triangle's plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville.
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.
In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle △ABC is the center of gravity of a homogeneous wire frame in the shape of △ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
In Euclidean geometry, the Apollonius point is a triangle center designated as X(181) in Clark Kimberling's Encyclopedia of Triangle Centers (ETC). It is defined as the point of concurrence of the three line segments joining each vertex of the triangle to the points of tangency formed by the opposing excircle and a larger circle that is tangent to all three excircles.
In geometry, the Exeter point is a special point associated with a plane triangle. The Exeter point is a triangle center and is designated as the center X(22) in Clark Kimberling's Encyclopedia of Triangle Centers. This was discovered in a computers-in-mathematics workshop at Phillips Exeter Academy in 1986. This is one of the recent triangle centers, unlike the classical triangle centers like centroid, incenter, and Steiner point.
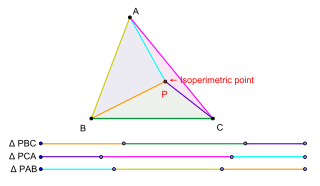
In geometry, the isoperimetric point is a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point P in the plane of a triangle ABC having the property that the triangles PBC, PCA and PAB have isoperimeters, that is, having the property that
In geometry the congruent isoscelizers point is a special point associated with a plane triangle. It is a triangle center and it is listed as X(173) in Clark Kimberling's Encyclopedia of Triangle Centers. This point was introduced to the study of triangle geometry by Peter Yff in 1989.
In geometry, the equal parallelians point is a special point associated with a plane triangle. It is a triangle center and it is denoted by X(192) in Clark Kimberling's Encyclopedia of Triangle Centers. There is a reference to this point in one of Peter Yff's notebooks, written in 1961.

In geometry the Morley centers are two special points associated with a plane triangle. Both of them are triangle centers. One of them called first Morley center is designated as X(356) in Clark Kimberling's Encyclopedia of Triangle Centers, while the other point called second Morley center is designated as X(357). The two points are also related to Morley's trisector theorem which was discovered by Frank Morley in around 1899.
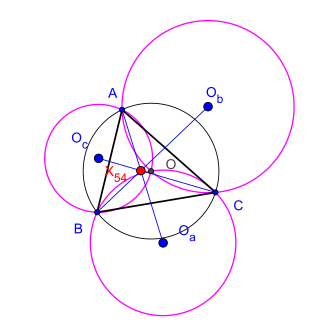
In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.
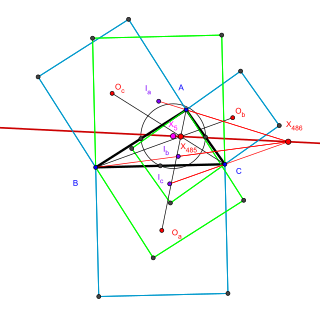
In the geometry of triangles, the Vecten points are two triangle centers associated with any triangle. They may be constructed by constructing three squares on the sides of the triangle, connecting each square centre by a line to the opposite triangle point, and finding the point where these three lines meet. The outer and inner Vecten points differ according to whether the squares are extended outward from the triangle sides, or inward.
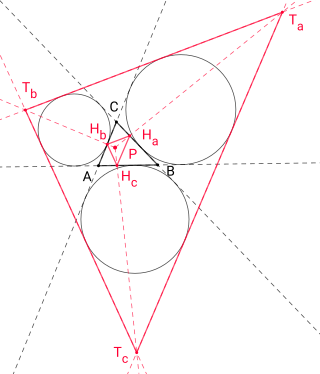
The Clawson point is a special point in a planar triangle defined by the trilinear coordinates , where are the interior angles at the triangle vertices . It is named after John Wentworth Clawson, who published it 1925 in the American Mathematical Monthly.












