John Edmark

Last updated

John Edmark (born 1965) [1] is an American designer, sculptor, and professor at Stanford University. Many of his art works take on a mathematical approach and application.

Contents

Education and career

Edmark graduated from Columbia University with a Bachelor of Science and later a Master of Science degree in Computer Science. [2] He then received a second Master of Science degree in Product Design at Stanford University. Throughout his life, he has acquired supplemental knowledge on architecture, art, and animation that can be reflected in his artwork. [3] His curiosities in mathematics — specifically spiral geometry — have also played a large influence on his art.

Edmark worked at Bell Labs for a few years researching computer graphics and virtual environments. [4] However, he cites that he preferred to create physical, tangible objects rather than virtual objects, which ultimately inspired him to create sculptures.[ citation needed ]

Currently, Edmark is a professor at Stanford University, where he lectures on topics such as design, art history, and mechanical engineering. [5] Edmark has also since created commissioned artwork for the Exploratorium, San Jose Museum of Art, Phaeno Science Center, and Swiss Science Center Technorama. [6]

Works

Edmark has been praised for his mathematical approach to art. One of his main goals is to strike curiosity and wonder in the observers. Much of his work is constructed based on intricate mathematical processes, as he describes his sculptures as “instruments that amplify our awareness of the sometimes tenuous relationship between facts and perception." [7]

One of his main focuses is on spiraling sculptures that create a blooming effect when spun and placed under a strobe light, similar to how zoetropes function. These "bloom" sculptures utilize mathematical patterns such as phyllotactic spirals and symmetry, which are both a part of spiral geometry. [8] His blooms, in particular, are inspired by mathematical processes occurring in nature, such as with pinecones and artichokes. [4] The petals of his "bloom" sculptures are placed 137.5° (golden angle) apart — based on properties from the golden ratio and the Fibonacci Sequence — in order to create the spiral effect when spun. His sculptures are 3D printed and are composed mostly of plywood, polypropylene, and brass. Edmark also creates animations based on these structures through taking a picture every 137.5° rotation. [9]

Other than his blooms, many of his sculptures are based on similar idea of spirals. For example, he has created a helicone, which is a wooden model replicating DNA strands that can be rotated by 68.75°. [10] His ''Fibonacci Tiling'' (2016) is a set of tiles that have pieces of similar shapes, but each tile is different in size. [11] The illusion of the sculpture spinning is created when pieces are added quickly.[ citation needed ]

Related Research Articles

<span class="mw-page-title-main">Golden ratio</span> Number, approximately 1.618

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if

<span class="mw-page-title-main">Fibonacci</span> Italian mathematician (c. 1170–1245)

Fibonacci, also known as Leonardo Bonacci, Leonardo of Pisa, or Leonardo Bigollo Pisano, was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".

<span class="mw-page-title-main">Fractal art</span> Form of algorithmic art

Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.

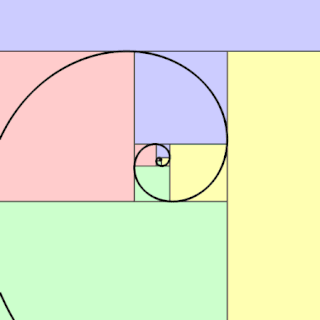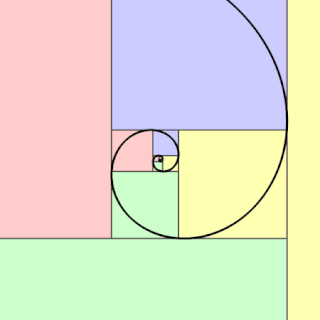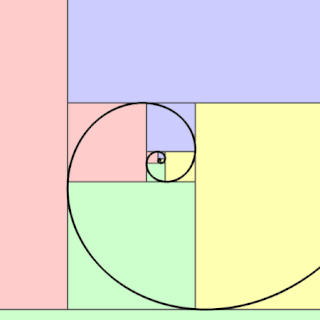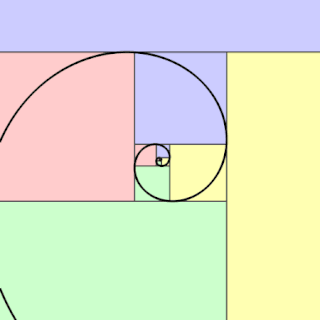
<span class="mw-page-title-main">Golden spiral</span> Self-similar curve related to golden ratio

In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider by a factor of φ for every quarter turn it makes.

<span class="mw-page-title-main">Utah teapot</span> Computer graphics 3D reference and test model

The Utah teapot, or the Newell teapot, is a 3D test model that has become a standard reference object and an in-joke within the computer graphics community. It is a mathematical model of an ordinary Melitta-brand teapot that appears solid with a nearly rotationally symmetrical body. Using a teapot model is considered the 3D equivalent of a "Hello, World!" program, a way to create an easy 3D scene with a somewhat complex model acting as the basic geometry for a scene with a light setup. Some programming libraries, such as the OpenGL Utility Toolkit, even have functions dedicated to drawing teapots.

<span class="mw-page-title-main">Tessellation</span> Tiling of a plane in mathematics

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

<span class="mw-page-title-main">Phyllotaxis</span> Arrangement of leaves on the stem of a plant

In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem. Phyllotactic spirals form a distinctive class of patterns in nature.

<span class="mw-page-title-main">Romanesco broccoli</span> Vegetable, member of the cabbage family

Romanesco broccoli is in fact a cultivar of the cauliflower, not a broccoli. It is an edible flower bud of the species Brassica oleracea, which also includes regular broccoli and cauliflower. It is chartreuse in color and has a striking form that naturally approximates a fractal. Romanesco has a nutty flavor and a firmer texture than white cauliflower or broccoli when cooked.

<span class="mw-page-title-main">3D computer graphics</span> Graphics that use a three-dimensional representation of geometric data

3D computer graphics, sometimes called CGI, 3-D-CGI or three-dimensional computer graphics, are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering digital images, usually 2D images but sometimes 3D images. The resulting images may be stored for viewing later or displayed in real time.

<span class="mw-page-title-main">Computer graphics (computer science)</span> Sub-field of computer science

Computer graphics is a sub-field of computer science which studies methods for digitally synthesizing and manipulating visual content. Although the term often refers to the study of three-dimensional computer graphics, it also encompasses two-dimensional graphics and image processing.

<span class="mw-page-title-main">Computer graphics</span> Graphics created using computers

Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. A great deal of specialized hardware and software has been developed, with the displays of most devices being driven by computer graphics hardware. It is a vast and recently developed area of computer science. The phrase was coined in 1960 by computer graphics researchers Verne Hudson and William Fetter of Boeing. It is often abbreviated as CG, or typically in the context of film as computer generated imagery (CGI). The non-artistic aspects of computer graphics are the subject of computer science research.

<span class="mw-page-title-main">Mathematical beauty</span> Aesthetic value of mathematics

Mathematical beauty is the aesthetic pleasure derived from the abstractness, purity, simplicity, depth or orderliness of mathematics. Mathematicians may express this pleasure by describing mathematics as beautiful or describe mathematics as an art form, or, at a minimum, as a creative activity.

<span class="mw-page-title-main">Mathematics and art</span> Relationship between mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

<span class="mw-page-title-main">3D modeling</span> Form of computer-aided engineering

In 3D computer graphics, 3D modeling is the process of developing a mathematical coordinate-based representation of a surface of an object in three dimensions via specialized software by manipulating edges, vertices, and polygons in a simulated 3D space.

<span class="mw-page-title-main">Patterns in nature</span> Visible regularity of form found in the natural world

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

<span class="mw-page-title-main">Garden of Archimedes</span> Mathematics museum in Via San Bartolo a Cintoia , Firenze

The Garden of Archimedes is a museum for mathematics in Florence, Italy, founded in 2004. It has been compared to the National Museum of Mathematics in New York City, the only museum in North America devoted to mathematics.

<span class="mw-page-title-main">Vandorn Hinnant</span>

Vandorn Hinnant is a visual artist, poet and educator based in Durham, North Carolina.

<span class="mw-page-title-main">Antonio Peticov</span> Brazilian painter, designer, sculptor, and engraver

Antonio Peticov is a Brazilian painter, designer, sculptor, and engraver.

<span class="mw-page-title-main">Henry Segerman</span> British-American mathematician (born 1979)

Henry Segerman is an Associate Professor of mathematics at Oklahoma State University in Stillwater, Oklahoma who does research in three-dimensional geometry and topology, especially three-manifolds, triangulations and hyperbolic geometry.

Edmund Orme Harriss is a British mathematician, writer and artist. Since 2010 he has been at the Fulbright College of Arts & Sciences at The University of Arkansas in Fayetteville, Arkansas where he is an Assistant Professor of Arts & Sciences (ARSC) and Mathematical Sciences (MASC). He does research in the Geometry of Tilings and Patterns, a branch of Convex and Discrete Geometry. He is the discoverer of the spiral that bears his name.

References

  1. ↑ "John Edmark | San José Museum of Art". sjmusart.org. October 2, 2014. Retrieved December 23, 2023.
  2. ↑ Wallace, Rebecca. "From the studio to the gallery". www.paloaltoonline.com. Retrieved December 23, 2023.
  3. ↑ "John Edmark". issuu. Retrieved December 23, 2023.
  4. 1 2 "The Infinite 3D Sculptures of John Edmark". Art of Play. Retrieved December 23, 2023.
  5. ↑ "John Edmark | Product Realization Lab". productrealization.stanford.edu. Retrieved December 23, 2023.
  6. ↑ "John Edmark". Riyadh Art. Retrieved December 23, 2023.
  7. ↑ Jobson, Christopher (May 5, 2017). "Creating The Never-Ending Bloom: The Amazing Mathematical Wonders of John Edmark". Colossal. Retrieved December 23, 2023.
  8. ↑ "John Edmark's Mathematical Sculptures". National Math Festival. November 20, 2020. Retrieved December 23, 2023.
  9. ↑ "Flourish (Bloom)". Exploratorium.
  10. ↑ "The Helicone: Science or Art? Plenty of Both" . Retrieved December 23, 2023.
  11. ↑ Arnold, Caitlin, The Big, Complicated Process of John Edmark’s Intriguing and Beautiful Bloom Spirals , retrieved December 23, 2023
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.