
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or .
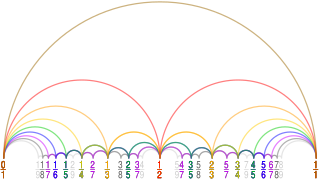
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions, either between 0 and 1, or without this restriction, which when in lowest terms have denominators less than or equal to n, arranged in order of increasing size.
In probability theory, the Chernoff bound, named after Herman Chernoff but due to Herman Rubin, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is a sharper bound than the known first- or second-moment-based tail bounds such as Markov's inequality or Chebyshev's inequality, which only yield power-law bounds on tail decay. However, the Chernoff bound requires that the variates be independent – a condition that neither Markov's inequality nor Chebyshev's inequality require, although Chebyshev's inequality does require the variates to be pairwise independent.
In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of all block codes in a unified way. Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another.
In mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of all possible words. It gives an important limitation on the efficiency with which any error-correcting code can utilize the space in which its code words are embedded. A code that attains the Hamming bound is said to be a perfect code.
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. It was first proved by Euclid in his work Elements. There are several proofs of the theorem.
In information theory, the noisy-channel coding theorem, establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel. This result was presented by Claude Shannon in 1948 and was based in part on earlier work and ideas of Harry Nyquist and Ralph Hartley.
In the mathematics of coding theory, the Plotkin bound, named after Morris Plotkin, is a limit on the maximum possible number of codewords in binary codes of given length n and given minimum distance d.
In information theory, information dimension is an information measure for random vectors in Euclidean space, based on the normalized entropy of finely quantized versions of the random vectors. This concept was first introduced by Alfréd Rényi in 1959.

In coding theory and information theory, a Z-channel is a communications channel used to model the behaviour of some data storage systems.
In mathematics, a Beatty sequence is the sequence of integers found by taking the floor of the positive multiples of a positive irrational number. Beatty sequences are named after Samuel Beatty, who wrote about them in 1926.
In mathematics, Abel's summation formula, introduced by Niels Henrik Abel, is intensively used in number theory and the study of special functions to compute series.
In mathematics, a cyclic polytope, denoted C(n,d), is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others. They play an important role in polyhedral combinatorics: according to the upper bound theorem, proved by Peter McMullen and Richard Stanley, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number fi of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.
AN codes are error-correcting code that are used in arithmetic applications. Arithmetic codes were commonly used in computer processors to ensure the accuracy of its arithmetic operations when electronics were more unreliable. Arithmetic codes help the processor to detect when an error is made and correct it. Without these codes, processors would be unreliable since any errors would go undetected. AN codes are arithmetic codes that are named for the integers and that are used to encode and decode the codewords.
In stochastic analysis, a rough path is a generalization of the notion of smooth path allowing to construct a robust solution theory for controlled differential equations driven by classically irregular signals, for example a Wiener process. The theory was developed in the 1990s by Terry Lyons. Several accounts of the theory are available.
In mathematics, the upper bound theorem states that cyclic polytopes have the largest possible number of faces among all convex polytopes with a given dimension and number of vertices. It is one of the central results of polyhedral combinatorics.
In number theory, the prime omega functions and count the number of prime factors of a natural number Thereby counts each distinct prime factor, whereas the related function counts the total number of prime factors of honoring their multiplicity. For example, if we have a prime factorization of of the form for distinct primes , then the respective prime omega functions are given by and . These prime factor counting functions have many important number theoretic relations.
In computer science, merge-insertion sort or the Ford–Johnson algorithm is a comparison sorting algorithm published in 1959 by L. R. Ford Jr. and Selmer M. Johnson. It uses fewer comparisons in the worst case than the best previously known algorithms, binary insertion sort and merge sort, and for 20 years it was the sorting algorithm with the fewest known comparisons. Although not of practical significance, it remains of theoretical interest in connection with the problem of sorting with a minimum number of comparisons. The same algorithm may have also been independently discovered by Stanisław Trybuła and Czen Ping.
































