Related Research Articles

In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. The term confluent refers to the merging of singular points of families of differential equations; confluere is Latin for "to flow together". There are several common standard forms of confluent hypergeometric functions:
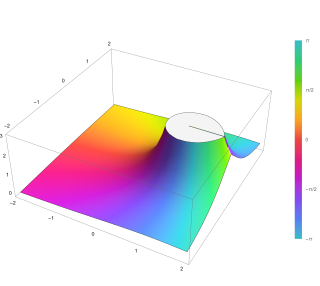
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
In mathematics, basic hypergeometric series, or q-hypergeometric series, are q-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.

Richard Allen Askey was an American mathematician, known for his expertise in the area of special functions. The Askey–Wilson polynomials are on the top level of the Askey scheme, which organizes orthogonal polynomials of hypergeometric type into a hierarchy. The Askey–Gasper inequality for Jacobi polynomials is essential in de Brange's famous proof of the Bieberbach conjecture.
In mathematics, the Selberg integral is a generalization of Euler beta function to n dimensions introduced by Atle Selberg (1944).
In mathematics, the q-Racah polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by Askey & Wilson (1979). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, Stieltjes–Wigert polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, for the weight function
In mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in Andrews & Askey (1985), the Askey scheme was first drawn by Labelle (1985) and by Askey and Wilson (1985), and has since been extended by Koekoek & Swarttouw (1998) and Koekoek, Lesky & Swarttouw (2010) to cover basic orthogonal polynomials.

In mathematics, the continuous dual Hahn polynomials are a family of orthogonal polynomials in the Askey scheme of hypergeometric orthogonal polynomials. They are defined in terms of generalized hypergeometric functions by
In mathematics, the continuous q-Hahn polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, the Al-Salam–Chihara polynomialsQn(x;a,b;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by Al-Salam and Chihara (1976). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14.8) give a detailed list of the properties of Al-Salam–Chihara polynomials.
The Reverend Frank Hilton Jackson was an English clergyman and mathematician who worked on basic hypergeometric series. He introduced several q-analogs such as the Jackson–Bessel functions, the Jackson-Hahn-Cigler q-addition, the Jackson derivative, and the Jackson integral.
In mathematics, the little q-Jacobi polynomialspn(x;a,b;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by Hahn (1949). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, the continuous q-Jacobi polynomialsP(α,β)
n(x|q), introduced by Askey & Wilson (1985), are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, the continuous big q-Hermite polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, the continuous q-Laguerre polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
Vadim V. Schechtman is a Russian mathematician who teaches in Toulouse.
Validated numerics, or rigorous computation, verified computation, reliable computation, numerical verification is numerics including mathematically strict error evaluation, and it is one field of numerical analysis. For computation, interval arithmetic is used, and all results are represented by intervals. Validated numerics were used by Warwick Tucker in order to solve the 14th of Smale's problems, and today it is recognized as a powerful tool for the study of dynamical systems.
Mikhail Kapranov, is a Russian mathematician, specializing in algebraic geometry, representation theory, mathematical physics, and category theory. He is currently a professor of the Kavli Institute for the Physics and Mathematics of the Universe at the University of Tokyo.
References
- Kita, Michitake; Aomoto, Kazuhiko (2011), Theory of hypergeometric functions, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-4-431-53912-4, MR 2799182