Kelvin–Voigt material

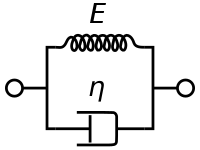
A Kelvin-Voigt material, also called a Voigt material, is the most simple model viscoelastic material showing typical rubbery properties. It is purely elastic on long timescales (slow deformation), but shows additional resistance to fast deformation. The model was developed independently by the British physicist Lord Kelvin ^[1] in 1865 and by the German physicist Woldemar Voigt ^[2] in 1890. ^[3]

Definition

Schematic representation of Kelvin–Voigt model.

The Kelvin-Voigt model, also called the Voigt model, is represented by a purely viscous damper and purely elastic spring connected in parallel as shown in the picture.

If, instead, we connect these two elements in series we get a model of a Maxwell material.

Since the two components of the model are arranged in parallel, the strains in each component are identical:

${\displaystyle \varepsilon _{\text{Total}}=\varepsilon _{\rm {S}}=\varepsilon _{\rm {D}}.}$

where the subscript D indicates the stress-strain in the damper and the subscript S indicates the stress-strain in the spring. Similarly, the total stress will be the sum of the stress in each component: ^[4]

${\displaystyle \sigma _{\text{Total}}=\sigma _{\rm {S}}+\sigma _{\rm {D}}.}$

From these equations we get that in a Kelvin-Voigt material, stress σ, strain ε and their rates of change with respect to time t are governed by equations of the form:

${\displaystyle \sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{dt}},}$

or, in dot notation:

${\displaystyle \sigma =E\varepsilon +\eta {\dot {\varepsilon }},}$

where E is a modulus of elasticity and ${\displaystyle \eta }$ is the viscosity. The equation can be applied either to the shear stress or normal stress of a material.

Effect of a sudden stress

Dependence of dimensionless deformation upon dimensionless time under constant stress

If we suddenly apply some constant stress ${\displaystyle \sigma _{0}}$ to Kelvin-Voigt material, then the deformations would approach the deformation for the pure elastic material ${\displaystyle \sigma _{0}/E}$ with the difference decaying exponentially: ^[4]

${\displaystyle \varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t/\tau _{R}}),}$

where t is time and ${\displaystyle \tau _{R}={\frac {\eta }{E}}}$ is the retardation time.

If we would free the material at time ${\displaystyle t_{1}}$, then the elastic element would retard the material back until the deformation becomes zero. The retardation obeys the following equation:

${\displaystyle \varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.}$

The picture shows the dependence of the dimensionless deformation ${\displaystyle {\frac {E\varepsilon (t)}{\sigma _{0}}}}$ on dimensionless time ${\displaystyle t/\tau _{R}}$. In the picture the stress on the material is loaded at time ${\displaystyle t=0}$, and released at the later dimensionless time ${\displaystyle t_{1}^{*}=t_{1}/\tau _{R}}$.

Since all the deformation is reversible (though not suddenly) the Kelvin–Voigt material is a solid.

The Voigt model predicts creep more realistically than the Maxwell model, because in the infinite time limit the strain approaches a constant:

${\displaystyle \lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},}$

while a Maxwell model predicts a linear relationship between strain and time, which is most often not the case. Although the Kelvin-Voigt model is effective for predicting creep, it is not good at describing the relaxation behavior after the stress load is removed.

Dynamic modulus

The complex dynamic modulus of the Kelvin-Voigt material is given by:

${\displaystyle E^{\star }(\omega )=E_{0}(1+i\omega \tau ).}$

Thus, the real and imaginary components of the dynamic modulus are referred to as storage modulus ${\displaystyle E^{\prime }}$ and ${\displaystyle E^{\prime \prime }}$ respectively:

${\displaystyle E^{\prime }=\Re [E^{\star }(\omega )],}$

${\displaystyle E^{\prime \prime }=\Im [E^{\star }(\omega )]=E_{0}\omega \tau .}$

Note that ${\displaystyle E^{\prime }}$ is constant, while ${\displaystyle E^{\prime \prime }}$ is directly proportional to frequency (where time-scale ${\displaystyle \tau }$ is the constant of proportionality). Often, this constant ${\displaystyle \tau }$ multiplied with angular frequency ${\displaystyle \omega }$ is called the loss modulus ${\displaystyle \eta =\omega \tau }$.

References

1. "IV. On the elasticity and viscosity of metals". Proceedings of the Royal Society of London. 14: 289–297. 1865-12-31. doi:10.1098/rspl.1865.0052. ISSN   0370-1662.
2. Voigt, Woldermar (1890). "Ueber die innere Reibung der festen Körper, insbesondere der Krystalle". Abhandlungen der Königlichen Gesellschaft von Wissenschaften zu Göttingen (in German). 36: 3–47.
3. Rajagopal, K.R. (2009). "A note on a reappraisal and generalization of the Kelvin–Voigt model". Mechanics Research Communications. 36 (2): 232–235. doi:10.1016/j.mechrescom.2008.09.005.
4. Meyers, Marc André; Chawla, Krishan Kumar (1999). "Section 13.11". Mechanical Behavior of Materials. Cambridge University Press. pp. 570–580. ISBN   978-1-107-39418-6.

See also

• Burgers material
• Generalized Maxwell model
• Maxwell material
• Standard linear solid model