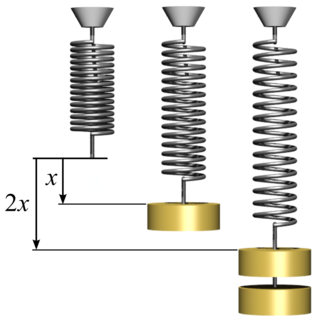
In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.
In engineering, deformation refers to the change in size or shape of an object. Displacements are the absolute change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the relative internal change in shape of an infinitesimal cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure by structural analysis.

In engineering and materials science, a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined. These curves reveal many of the properties of a material, such as the Young's modulus, the yield strength and the ultimate tensile strength.
Dynamic mechanical analysis is a technique used to study and characterize materials. It is most useful for studying the viscoelastic behavior of polymers. A sinusoidal stress is applied and the strain in the material is measured, allowing one to determine the complex modulus. The temperature of the sample or the frequency of the stress are often varied, leading to variations in the complex modulus; this approach can be used to locate the glass transition temperature of the material, as well as to identify transitions corresponding to other molecular motions.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.
Hemorheology, also spelled haemorheology, or blood rheology, is the study of flow properties of blood and its elements of plasma and cells. Proper tissue perfusion can occur only when blood's rheological properties are within certain levels. Alterations of these properties play significant roles in disease processes. Blood viscosity is determined by plasma viscosity, hematocrit and mechanical properties of red blood cells. Red blood cells have unique mechanical behavior, which can be discussed under the terms erythrocyte deformability and erythrocyte aggregation. Because of that, blood behaves as a non-Newtonian fluid. As such, the viscosity of blood varies with shear rate. Blood becomes less viscous at high shear rates like those experienced with increased flow such as during exercise or in peak-systole. Therefore, blood is a shear-thinning fluid. Contrarily, blood viscosity increases when shear rate goes down with increased vessel diameters or with low flow, such as downstream from an obstruction or in diastole. Blood viscosity also increases with increases in red cell aggregability.
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed.

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.
A Kelvin-Voigt material, also called a Voigt material, is the most simple model viscoelastic material showing typical rubbery properties. It is purely elastic on long timescales, but shows additional resistance to fast deformation. The model was developed independently by the British physicist Lord Kelvin in 1865 and by the German physicist Woldemar Voigt in 1890.
A Burgers material is a viscoelastic material having the properties both of elasticity and viscosity. It is named after the Dutch physicist Johannes Martinus Burgers.
Dynamic modulus is the ratio of stress to strain under vibratory conditions. It is a property of viscoelastic materials.
The J-integral represents a way to calculate the strain energy release rate, or work (energy) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by G. P. Cherepanov and independently in 1968 by James R. Rice, who showed that an energetic contour path integral was independent of the path around a crack.
The Ramberg–Osgood equation was created to describe the non linear relationship between stress and strain—that is, the stress–strain curve—in materials near their yield points. It is especially applicable to metals that harden with plastic deformation, showing a smooth elastic-plastic transition. As it is a phenomenological model, checking the fit of the model with actual experimental data for the particular material of interest is essential.
The standard linear solid (SLS), also known as the Zener model after Clarence Zener, is a method of modeling the behavior of a viscoelastic material using a linear combination of springs and dashpots to represent elastic and viscous components, respectively. Often, the simpler Maxwell model and the Kelvin–Voigt model are used. These models often prove insufficient, however; the Maxwell model does not describe creep or recovery, and the Kelvin–Voigt model does not describe stress relaxation. SLS is the simplest model that predicts both phenomena.
The Larson–Miller relation, also widely known as the Larson–Miller parameter and often abbreviated LMP, is a parametric relation used to extrapolate experimental data on creep and rupture life of engineering materials.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.

A fiber-reinforced composite (FRC) is a composite building material that consists of three components:
- the fibers as the discontinuous or dispersed phase,
- the matrix as the continuous phase, and
- the fine interphase region, also known as the interface.

Plasticity theory for rocks is concerned with the response of rocks to loads beyond the elastic limit. Historically, conventional wisdom has it that rock is brittle and fails by fracture while plasticity is identified with ductile materials. In field scale rock masses, structural discontinuities exist in the rock indicating that failure has taken place. Since the rock has not fallen apart, contrary to expectation of brittle behavior, clearly elasticity theory is not the last word.

Flow plasticity is a solid mechanics theory that is used to describe the plastic behavior of materials. Flow plasticity theories are characterized by the assumption that a flow rule exists that can be used to determine the amount of plastic deformation in the material.
Anelasticity is a property of materials that describes their behaviour when undergoing deformation. Its formal definition does not include the physical or atomistic mechanisms but still interprets the anelastic behaviour as a manifestation of internal relaxation processes. It is a behaviour differing from elastic behaviour.






































