
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals and minimizes the total weight of its edges. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices, thus it is "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

In mathematics and computational geometry, the Gabriel graph of a set of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph with vertex set in which any two distinct points and are adjacent precisely when the closed disc having as a diameter contains no other points. Another way of expressing the same adjacency criterion is that and should be the two closest given points to their midpoint, with no other given point being as close. Gabriel graphs naturally generalize to higher dimensions, with the empty disks replaced by empty closed balls. Gabriel graphs are named after K. Ruben Gabriel, who introduced them in a paper with Robert R. Sokal in 1969.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

The nearest neighbor graph (NNG) is a directed graph defined for a set of points in a metric space, such as the Euclidean distance in the plane. The NNG has a vertex for each point, and a directed edge from p to q whenever q is a nearest neighbor of p, a point whose distance from p is minimum among all the given points other than p itself.

In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points and by an edge whenever there does not exist a third point that is closer to both and than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.

In computational geometry, the Urquhart graph of a set of points in the plane, named after Roderick B. Urquhart, is obtained by removing the longest edge from each triangle in the Delaunay triangulation.
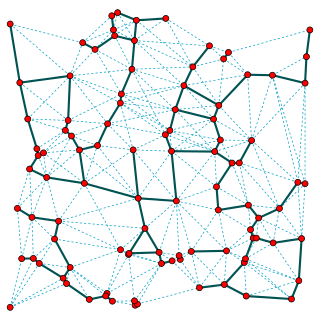
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.

In graph theory, the rectilinear minimum spanning tree (RMST) of a set of n points in the plane is a minimum spanning tree of that set, where the weight of the edge between each pair of points is the rectilinear distance between those two points.
A kinetic data structure is a data structure used to track an attribute of a geometric system that is moving continuously. For example, a kinetic convex hull data structure maintains the convex hull of a group of moving points. The development of kinetic data structures was motivated by computational geometry problems involving physical objects in continuous motion, such as collision or visibility detection in robotics, animation or computer graphics.
A kinetic closest pair data structure is a kinetic data structure that maintains the closest pair of points, given a set P of n points that are moving continuously with time in a metric space. While many efficient algorithms were known in the static case, they proved hard to kinetize, so new static algorithms were developed to solve this problem.
A kinetic smallest enclosing disk data structure is a kinetic data structure that maintains the smallest enclosing disk of a set of moving points.
A kinetic minimum spanning tree is a kinetic data structure that maintains the minimum spanning tree (MST) of a graph whose edge weights are changing as a continuous function of time.
The k-semi-Yao graph (k-SYG) of a set of n objects P is a geometric proximity graph, which was first described to present a kinetic data structure for maintenance of all the nearest neighbors on moving objects. It is named for its relation to the Yao graph, which is named after Andrew Yao.
Reverse-search algorithms are a class of algorithms for generating all objects of a given size, from certain classes of combinatorial objects. In many cases, these methods allow the objects to be generated in polynomial time per object, using only enough memory to store a constant number of objects. They work by organizing the objects to be generated into a spanning tree of their state space, and then performing a depth-first search of this tree.













