
In mathematics, particularly in complex analysis, a Riemann surface is a one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.
In mathematics, birational geometry is a field of algebraic geometry in which the goal is to determine when two algebraic varieties are isomorphic outside lower-dimensional subsets. This amounts to studying mappings that are given by rational functions rather than polynomials; the map may fail to be defined where the rational functions have poles.

In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2, 7), the second-smallest non-abelian simple group. The quartic was first described in.

In algebraic geometry, a hyperelliptic curve of genus g > 1 is an algebraic curve given by an equation of the form
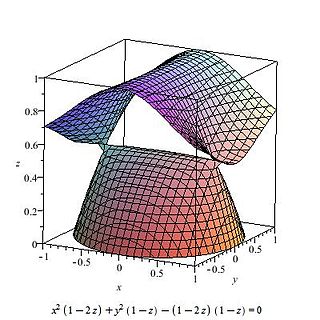
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single quaternary cubic polynomial which is homogeneous of degree 3. Cubic surfaces are del Pezzo surfaces.
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.
In mathematics, in the sub-field of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In mathematics, the Torelli theorem, named after Ruggiero Torelli, is a classical result of algebraic geometry over the complex number field, stating that a non-singular projective algebraic curve C is determined by its Jacobian variety J(C), when the latter is given in the form of a principally polarized abelian variety. In other words, the complex torus J(C), with certain 'markings', is enough to recover C. The same statement holds over any algebraically closed field. From more precise information on the constructed isomorphism of the curves it follows that if the canonically principally polarized Jacobian varieties of curves of genus are k-isomorphic for k any perfect field, so are the curves.
In mathematics, the intermediate Jacobian of a compact Kähler manifold or Hodge structure is a complex torus that is a common generalization of the Jacobian variety of a curve and the Picard variety and the Albanese variety. It is obtained by putting a complex structure on the torus Hn(M,R)/Hn(M,Z) for n odd. There are several different natural ways to put a complex structure on this torus, giving several different sorts of intermediate Jacobians, including one due to Weil (1952) and one due to Griffiths. The ones constructed by Weil have natural polarizations if M is projective, and so are abelian varieties, while the ones constructed by Griffiths behave well under holomorphic deformations.
In mathematics, Enriques surfaces are algebraic surfaces such that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square. Enriques surfaces are all projective and are elliptic surfaces of genus 0. Over fields of characteristic not 2 they are quotients of K3 surfaces by a group of order 2 acting without fixed points and their theory is similar to that of algebraic K3 surfaces. Enriques surfaces were first studied in detail by Enriques (1896) as an answer to a question discussed by Castelnuovo (1895) about whether a surface with q=pg = 0 is necessarily rational, though some of the Reye congruences introduced earlier by Reye (1882) are also examples of Enriques surfaces.
In algebraic geometry, a branch of mathematics, a Zariski surface is a surface over a field of characteristic p > 0 such that there is a dominant inseparable map of degree p from the projective plane to the surface. In particular, all Zariski surfaces are unirational. They were named by Piotr Blass in 1977 after Oscar Zariski who used them in 1958 to give examples of unirational surfaces in characteristic p > 0 that are not rational.
In algebraic geometry, a Fano surface is a surface of general type whose points index the lines on a non-singular cubic threefold. They were first studied by Fano (1904).
In mathematics, a cubic form is a homogeneous polynomial of degree 3, and a cubic hypersurface is the zero set of a cubic form. In the case of a cubic form in three variables, the zero set is a cubic plane curve.
In algebraic geometry, a supersingular K3 surface is a K3 surface over a field k of characteristic p > 0 such that the slopes of Frobenius on the crystalline cohomology H2(X,W ) are all equal to 1. These have also been called Artin supersingular K3 surfaces. Supersingular K3 surfaces can be considered the most special and interesting of all K3 surfaces.
In arithmetic geometry, the Tate–Shafarevich group Ш(A/K), introduced by Serge Lang and John Tate (1958) and Igor Shafarevich (1959), of an abelian variety A (or more generally a group scheme) defined over a number field K consists of the elements of the Weil–Châtelet group WC(A/K) = H1(GK, A) that become trivial in all of the completions of K (i.e. the p-adic fields obtained from K, as well as its real and complex completions). Thus, in terms of Galois cohomology, it can be written as

In mathematics, Bring's curve is the curve given by the equations

The American Journal of Mathematics is a bimonthly mathematics journal published by the Johns Hopkins University Press.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to identify objects uniquely, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.











