L(2, 1)-coloring is a particular case of L(h, k)-coloring. In an L(2, 1)-coloring of a graph, G, the vertices of G are assigned color numbers in such a way that adjacent vertices get labels that differ by at least two, and the vertices that are at a distance of two from each other get labels that differ by at least one. [1]
An L(2,1)-coloring is a proper coloring, since adjacent vertices are assigned distinct colors.
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.
In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.
In the mathematical discipline of graph theory, a graph labelling is the assignment of labels, traditionally represented by integers, to edges and/or vertices of a graph.
The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the countries of the world, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.
In graph theory, reachability refers to the ability to get from one vertex to another within a graph. A vertex can reach a vertex if there exists a sequence of adjacent vertices which starts with and ends with .
In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cube graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n – 1n edges, and is a regular graph with n edges touching each vertex.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
In graph theory, a mixed graphG = (V, E, A) is a graph consisting of a set of vertices V, a set of (undirected) edges E, and a set of directed edges (or arcs) A.
In graph theory, a total coloring is a coloring on the vertices and edges of a graph such that:
In graph theory, a branch of mathematics, a radio coloring of an undirected graph is a form of graph coloring in which one assigns positive integer labels to the graphs such that the labels of adjacent vertices differ by at least two, and the labels of vertices at distance two from each other differ by at least one. Radio coloring was first studied by Griggs & Yeh (1992), under a different name, L(2,1)-labeling. It was called radio coloring by Frank Harary because it models the problem of channel assignment in radio broadcasting, while avoiding electromagnetic interference between radio stations that are near each other both in the graph and in their assigned channel frequencies.
In graph theory, a L(h, k)-labelling, L(h, k)-coloring or sometimes L(p, q)-coloring is a (proper) vertex coloring in which every pair of adjacent vertices has color numbers that differ by at least h, and any nodes connected by a 2 length path have their colors differ by at least k. The parameters, h and k are understood to be non-negative integers.
In graph theory, interval edge coloring is a type of edge coloring in which edges are labeled by the integers in some interval, every integer in the interval is used by at least one edge, and at each vertex the labels that appear on incident edges form a consecutive set of distinct numbers.
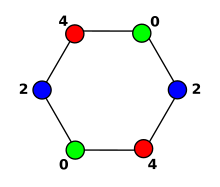
In graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that destroys all of the nontrivial symmetries of the graph. The coloring does not need to be a proper coloring: adjacent vertices are allowed to be given the same color. For the colored graph, there should not exist any one-to-one mapping of the vertices to themselves that preserves both adjacency and coloring. The minimum number of colors in a distinguishing coloring is called the distinguishing number of the graph.
Hamiltonian coloring, named after William Rowan Hamilton, is a type of graph coloring. Hamiltonian coloring uses a concept called detour distance between two vertices of the graph. It has many applications in different areas of science and technology.
In graph theory, a rainbow-independent set (ISR) is an independent set in a graph, in which each vertex has a different color.
 | This graph theory-related article is a stub. You can help Wikipedia by expanding it. |