Lagrange's identity

Last updated February 03, 2024

In algebra, Lagrange's identity, named after Joseph Louis Lagrange, is:^[1]^[2]

{\begin{aligned}\left(\sum _{k=1}^{n}a_{k}^{2}\right)\left(\sum _{k=1}^{n}b_{k}^{2}\right)-\left(\sum _{k=1}^{n}a_{k}b_{k}\right)^{2}&=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\\&\left(={\frac {1}{2}}\sum _{i=1}^{n}\sum _{j=1,j\neq i}^{n}(a_{i}b_{j}-a_{j}b_{i})^{2}\right),\end{aligned}}

which applies to any two sets {a₁, a₂, ..., a_n} and {b₁, b₂, ..., b_n} of real or complex numbers (or more generally, elements of a commutative ring). This identity is a generalisation of the Brahmagupta–Fibonacci identity and a special form of the Binet–Cauchy identity.

In a more compact vector notation, Lagrange's identity is expressed as:^[3]

\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}=\sum _{1\leq i<j\leq n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\,,

where a and b are n-dimensional vectors with components that are real numbers. The extension to complex numbers requires the interpretation of the dot product as an inner product or Hermitian dot product. Explicitly, for complex numbers, Lagrange's identity can be written in the form:^[4]

\left(\sum _{k=1}^{n}|a_{k}|^{2}\right)\left(\sum _{k=1}^{n}|b_{k}|^{2}\right)-\left|\sum _{k=1}^{n}a_{k}b_{k}\right|^{2}=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}\left|a_{i}{\overline {b}}_{j}-a_{j}{\overline {b}}_{i}\right|^{2}

involving the absolute value.^[5]^[6]

Since the right-hand side of the identity is clearly non-negative, it implies Cauchy's inequality in the finite-dimensional real coordinate space Rⁿ and its complex counterpart Cⁿ.

Geometrically, the identity asserts that the square of the volume of the parallelepiped spanned by a set of vectors is the Gram determinant of the vectors.

Lagrange's identity and exterior algebra

In terms of the wedge product, Lagrange's identity can be written

(a\cdot a)(b\cdot b)-(a\cdot b)^{2}=(a\wedge b)\cdot (a\wedge b).

Hence, it can be seen as a formula which gives the length of the wedge product of two vectors, which is the area of the parallelogram they define, in terms of the dot products of the two vectors, as

\|a\wedge b\|={\sqrt {(a\cdot a)(b\cdot b)-(a\cdot b)^{2}}}={\sqrt {\|a\|^{2}\|b\|^{2}-(a\cdot b)^{2}}}.

Lagrange's identity and vector calculus

In three dimensions, Lagrange's identity asserts that if a and b are vectors in R³ with lengths |a| and |b|, then Lagrange's identity can be written in terms of the cross product and dot product:^[7]^[8]

|\mathbf {a} |^{2}|\mathbf {b} |^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}=|\mathbf {a} \times \mathbf {b} |^{2}

Using the definition of angle based upon the dot product (see also Cauchy–Schwarz inequality), the left-hand side is

\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\left(1-\cos ^{2}\theta \right)=\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta

where $θ$ is the angle formed by the vectors a and b. The area of a parallelogram with sides $| a |$ and $| b |$ and angle $θ$ is known in elementary geometry to be

\left|\mathbf {a} \right|\left|\mathbf {b} \right|\left|\sin \theta \right|,

so the left-hand side of Lagrange's identity is the squared area of the parallelogram. The cross product appearing on the right-hand side is defined by

\mathbf {a} \times \mathbf {b} =\left(a_{2}b_{3}-a_{3}b_{2}\right)\mathbf {i} +\left(a_{3}b_{1}-a_{1}b_{3}\right)\mathbf {j} +\left(a_{1}b_{2}-a_{2}b_{1}\right)\mathbf {k}

which is a vector whose components are equal in magnitude to the areas of the projections of the parallelogram onto the yz, zx, and xy planes, respectively.

Seven dimensions

For a and b as vectors in R⁷, Lagrange's identity takes on the same form as in the case of R³^[9]

|\mathbf {a} |^{2}|\mathbf {b} |^{2}-|\mathbf {a} \cdot \mathbf {b} |^{2}=|\mathbf {a} \times \mathbf {b} |^{2}\ ,

However, the cross product in 7 dimensions does not share all the properties of the cross product in 3 dimensions. For example, the direction of a × b in 7-dimensions may be the same as c × d even though c and d are linearly independent of a and b. Also the seven-dimensional cross product is not compatible with the Jacobi identity.^[9]

Quaternions

A quaternion p is defined as the sum of a scalar t and a vector v:

p=t+\mathbf {v} =t+x\ \mathbf {i} +y\ \mathbf {j} +z\ \mathbf {k} .

The product of two quaternions $p = t + v$ and $q = s + w$ is defined by

pq=(st-\mathbf {v} \cdot \mathbf {w} )+s\ \mathbf {v} +t\ \mathbf {w} +\mathbf {v} \times \mathbf {w} .

The quaternionic conjugate of q is defined by

{\overline {q}}=t-\mathbf {v} ,

and the norm squared is

|q|^{2}=q{\overline {q}}=t^{2}\ +\ x^{2}+\ y^{2}\ +\ z^{2}.

The multiplicativity of the norm in the quaternion algebra provides, for quaternions p and q:^[10]

\left|pq\right|=\left|p\right|\left|q\right|.

The quaternions p and q are called imaginary if their scalar part is zero; equivalently, if

p=\mathbf {v} ,\quad q=\mathbf {w} .

Lagrange's identity is just the multiplicativity of the norm of imaginary quaternions,

|\mathbf {v} \mathbf {w} |^{2}=|\mathbf {v} |^{2}|\mathbf {w} |^{2},

since, by definition,

|\mathbf {v} \mathbf {w} |^{2}=(\mathbf {v} \cdot \mathbf {w} )^{2}+|\mathbf {v} \times \mathbf {w} |^{2}.

Proof of algebraic form

The vector form follows from the Binet-Cauchy identity by setting c_i = a_i and d_i = b_i. The second version follows by letting c_i and d_i denote the complex conjugates of a_i and b_i, respectively,

Here is also a direct proof.^[11] The expansion of the first term on the left side is:

\left(\sum _{k=1}^{n}a_{k}^{2}\right)\left(\sum _{k=1}^{n}b_{k}^{2}\right)=\sum _{i=1}^{n}\sum _{j=1}^{n}a_{i}^{2}b_{j}^{2}=\sum _{k=1}^{n}a_{k}^{2}b_{k}^{2}+\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}^{2}b_{j}^{2}+\sum _{j=1}^{n-1}\sum _{i=j+1}^{n}a_{i}^{2}b_{j}^{2}\ ,

(1)

which means that the product of a column of as and a row of bs yields (a sum of elements of) a square of abs, which can be broken up into a diagonal and a pair of triangles on either side of the diagonal.

The second term on the left side of Lagrange's identity can be expanded as:

\left(\sum _{k=1}^{n}a_{k}b_{k}\right)^{2}=\sum _{k=1}^{n}a_{k}^{2}b_{k}^{2}+2\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}b_{i}a_{j}b_{j}\,,

(2)

which means that a symmetric square can be broken up into its diagonal and a pair of equal triangles on either side of the diagonal.

To expand the summation on the right side of Lagrange's identity, first expand the square within the summation:

\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}(a_{i}b_{j}-a_{j}b_{i})^{2}=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}\left(a_{i}^{2}b_{j}^{2}+a_{j}^{2}b_{i}^{2}-2a_{i}b_{j}a_{j}b_{i}\right).

Distribute the summation on the right side,

\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}(a_{i}b_{j}-a_{j}b_{i})^{2}=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}^{2}b_{j}^{2}+\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{j}^{2}b_{i}^{2}-2\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}b_{j}a_{j}b_{i}.

Now exchange the indices i and j of the second term on the right side, and permute the b factors of the third term, yielding:

\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}(a_{i}b_{j}-a_{j}b_{i})^{2}=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}^{2}b_{j}^{2}+\sum _{j=1}^{n-1}\sum _{i=j+1}^{n}a_{i}^{2}b_{j}^{2}-2\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}b_{i}a_{j}b_{j}\ .

(3)

Back to the left side of Lagrange's identity: it has two terms, given in expanded form by Equations ( 1 ) and ( 2 ). The first term on the right side of Equation ( 2 ) ends up canceling out the first term on the right side of Equation ( 1 ), yielding

\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}^{2}b_{j}^{2}+\sum _{j=1}^{n-1}\sum _{i=j+1}^{n}a_{i}^{2}b_{j}^{2}-2\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}a_{i}b_{i}a_{j}b_{j}

( 1 ) − ( 2 )

which is the same as Equation ( 3 ), so Lagrange's identity is indeed an identity, Q.E.D.

Proof of Lagrange's identity for complex numbers

Normed division algebras require that the norm of the product is equal to the product of the norms. Lagrange's identity exhibits this equality. The product identity used as a starting point here, is a consequence of the norm of the product equality with the product of the norm for scator algebras. This proposal, originally presented in the context of a deformed Lorentz metric, is based on a transformation stemming from the product operation and magnitude definition in hyperbolic scator algebra.^[12] Lagrange's identity can be proved in a variety of ways.^[4] Most derivations use the identity as a starting point and prove in one way or another that the equality is true. In the present approach, Lagrange's identity is actually derived without assuming it a priori.^{[ citation needed ]}

Let $a_{i},b_{i}\in \mathbb {C}$ be complex numbers and the overbar represents complex conjugate.

The product identity

\prod _{i=1}^{n}\left(1-a_{i}{\bar {a}}_{i}-b_{i}{\bar {b}}_{i}+a_{i}{\bar {a}}_{i}b_{i}{\bar {b}}_{i}\right)=\prod _{i=1}^{n}\left(1-a_{i}{\bar {a}}_{i}\right)\prod _{i=1}^{n}\left(1-b_{i}{\bar {b}}_{i}\right)

reduces to the complex Lagrange's identity when fourth order terms, in a series expansion, are considered.

In order to prove it, expand the product on the LHS of the product identity in terms of series up to fourth order. To this end, recall that products of the form $\left(1+x_{i}\right)$ can be expanded in terms of sums as

\prod _{i=1}^{n}\left(1+x_{i}\right)=1+\sum _{i=1}^{n}x_{i}+\sum _{i<j}^{n}x_{i}x_{j}+{\mathcal {O}}^{3+}(x),

where ${\mathcal {O}}^{3+}(x)$ means terms with order three or higher in $x$ .

\prod _{i=1}^{n}\left(1-a_{i}{\bar {a}}_{i}-b_{i}{\bar {b}}_{i}+a_{i}{\bar {a}}_{i}b_{i}{\bar {b}}_{i}\right)=1-\sum _{i=1}^{n}\left(a_{i}{\bar {a}}_{i}+b_{i}{\bar {b}}_{i}\right)+\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}b_{i}{\bar {b}}_{i}+\sum _{i<j}^{n}\left(a_{i}{\bar {a}}_{i}a_{j}{\bar {a}}_{j}+b_{i}{\bar {b}}_{i}b_{j}{\bar {b}}_{j}\right)+\sum _{i<j}^{n}\left(a_{i}{\bar {a}}_{i}b_{j}{\bar {b}}_{j}+a_{j}{\bar {a}}_{j}b_{i}{\bar {b}}_{i}\right)+{\mathcal {O}}^{5+}.

The two factors on the RHS are also written in terms of series

\prod _{i=1}^{n}\left(1-a_{i}{\bar {a}}_{i}\right)\prod _{i=1}^{n}\left(1-b_{i}{\bar {b}}_{i}\right)=\left(1-\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}+\sum _{i<j}^{n}a_{i}{\bar {a}}_{i}a_{j}{\bar {a}}_{j}+{\mathcal {O}}^{5+}\right)\left(1-\sum _{i=1}^{n}b_{i}{\bar {b}}_{i}+\sum _{i<j}^{n}b_{i}{\bar {b}}_{i}b_{j}{\bar {b}}_{j}+{\mathcal {O}}^{5+}\right).

The product of this expression up to fourth order is

\prod _{i=1}^{n}\left(1-a_{i}{\bar {a}}_{i}\right)\prod _{i=1}^{n}\left(1-b_{i}{\bar {b}}_{i}\right)=1-\sum _{i=1}^{n}\left(a_{i}{\bar {a}}_{i}+b_{i}{\bar {b}}_{i}\right)+\left(\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}\right)\left(\sum _{i=1}^{n}b_{i}{\bar {b}}_{i}\right)+\sum _{i<j}^{n}\left(a_{i}{\bar {a}}_{i}a_{j}{\bar {a}}_{j}+b_{i}{\bar {b}}_{i}b_{j}{\bar {b}}_{j}\right)+{\mathcal {O}}^{5+}.

Substitution of these two results in the product identity give

\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}b_{i}{\bar {b}}_{i}+\sum _{i<j}^{n}\left(a_{i}{\bar {a}}_{i}b_{j}{\bar {b}}_{j}+a_{j}{\bar {a}}_{j}b_{i}{\bar {b}}_{i}\right)=\left(\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}\right)\left(\sum _{i=1}^{n}b_{i}{\bar {b}}_{i}\right).

The product of two conjugates series can be expressed as series involving the product of conjugate terms. The conjugate series product is

\left(\sum _{i=1}^{n}x_{i}\right)\left(\sum _{i=1}^{n}{\bar {x}}_{i}\right)=\sum _{i=1}^{n}x_{i}{\bar {x}}_{i}+\sum _{i<j}^{n}\left(x_{i}{\bar {x}}_{j}+{\bar {x}}_{i}x_{j}\right),

thus

\left(\sum _{i=1}^{n}a_{i}b_{i}\right)\left(\sum _{i=1}^{n}{\overline {a_{i}b_{i}}}\right)-\sum _{i<j}^{n}\left(a_{i}b_{i}{\bar {a}}_{j}{\bar {b}}_{j}+{\bar {a}}_{i}{\bar {b}}_{i}a_{j}b_{j}\right)+\sum _{i<j}^{n}\left(a_{i}{\bar {a}}_{i}b_{j}{\bar {b}}_{j}+a_{j}{\bar {a}}_{j}b_{i}{\bar {b}}_{i}\right)=\left(\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}\right)\left(\sum _{i=1}^{n}b_{i}{\bar {b}}_{i}\right).

The terms of the last two series on the LHS are grouped as

a_{i}{\bar {a}}_{i}b_{j}{\bar {b}}_{j}+a_{j}{\bar {a}}_{j}b_{i}{\bar {b}}_{i}-a_{i}b_{i}{\bar {a}}_{j}{\bar {b}}_{j}-{\bar {a}}_{i}{\bar {b}}_{i}a_{j}b_{j}=\left(a_{i}{\bar {b}}_{j}-a_{j}{\bar {b}}_{i}\right)\left({\bar {a}}_{i}b_{j}-{\bar {a}}_{j}b_{i}\right),

in order to obtain the complex Lagrange's identity:

\left(\sum _{i=1}^{n}a_{i}b_{i}\right)\left(\sum _{i=1}^{n}{\overline {a_{i}b_{i}}}\right)+\sum _{i<j}^{n}\left(a_{i}{\bar {b}}_{j}-a_{j}{\bar {b}}_{i}\right)\left({\overline {a_{i}{\bar {b}}_{j}-a_{j}{\bar {b}}_{i}}}\right)=\left(\sum _{i=1}^{n}a_{i}{\bar {a}}_{i}\right)\left(\sum _{i=1}^{n}b_{i}{\bar {b}}_{i}\right).

In terms of the moduli,

\left|\sum _{i=1}^{n}a_{i}b_{i}\right|^{2}+\sum _{i<j}^{n}\left|a_{i}{\bar {b}}_{j}-a_{j}{\bar {b}}_{i}\right|^{2}=\left(\sum _{i=1}^{n}\left|a_{i}\right|^{2}\right)\left(\sum _{i=1}^{n}\left|b_{i}\right|^{2}\right).

Lagrange's identity for complex numbers has been obtained from a straightforward product identity. A derivation for the reals is obviously even more succinct. Since the Cauchy–Schwarz inequality is a particular case of Lagrange's identity,^[4] this proof is yet another way to obtain the CS inequality. Higher order terms in the series produce novel identities.

Related Research Articles

In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. The determinant of a matrix $A$ is commonly denoted $det(A)$ , $det A$ , or $| A |$ . Its value characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants.

<span class="mw-page-title-main">Inner product space</span> Generalization of the dot product; used to define Hilbert spaces

In mathematics, an inner product space is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in $. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or scalar product of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces . The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.$

In mathematics, a product is the result of multiplication, or an expression that identifies objects to be multiplied, called factors. For example, 21 is the product of 3 and 7, and $is the product of and . When one factor is an integer, the product is called a multiple .$

The Cauchy–Schwarz inequality is an upper bound on the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics.

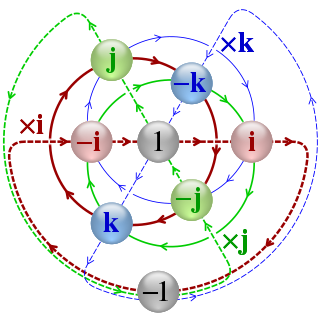
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by $H$ , or in blackboard bold by $Although multiplication of quaternions is noncommutative, it gives a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form$

In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol $. Given two linearly independent vectors a and b, the cross product, a \times b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.$

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers, and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space.

In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space $under the operation of composition.$

Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.

In vector calculus, Green's theorem relates a line integral around a simple closed curve $C$ to a double integral over the plane region $D$ bounded by $C$ . It is the two-dimensional special case of Stokes' theorem.

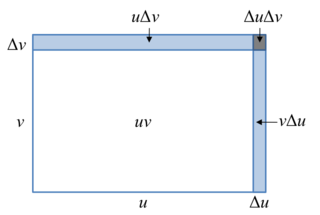
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as

In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring, and its basis is the set of elements of the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.

In mathematics, specifically linear algebra, the Cauchy–Binet formula, named after Augustin-Louis Cauchy and Jacques Philippe Marie Binet, is an identity for the determinant of the product of two rectangular matrices of transpose shapes. It generalizes the statement that the determinant of a product of square matrices is equal to the product of their determinants. The formula is valid for matrices with the entries from any commutative ring.

In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude of the vector. This norm can be defined as the square root of the inner product of a vector with itself.

In abstract algebra, the biquaternions are the numbers $w + x i + y j + z k$ , where $w, x, y$ , and $z$ are complex numbers, or variants thereof, and the elements of ${1, i, j, k}$ multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:

In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.

<span class="mw-page-title-main">Dual quaternion</span> Eight-dimensional algebra over the real numbers

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε² = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.

<span class="mw-page-title-main">Classical group</span>

In mathematics, the classical groups are defined as the special linear groups over the reals $R$ , the complex numbers $C$ and the quaternions $H$ together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph The Classical Groups.

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.

References

↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. ISBN 1-58488-347-2.
↑ Robert E Greene; Steven G Krantz (2006). "Exercise 16". Function theory of one complex variable (3rd ed.). American Mathematical Society. p. 22. ISBN 0-8218-3962-4.
↑ Vladimir A. Boichenko; Gennadiĭ Alekseevich Leonov; Volker Reitmann (2005). Dimension theory for ordinary differential equations. Vieweg+Teubner Verlag. p. 26. ISBN 3-519-00437-2.
1 2 3 J. Michael Steele (2004). "Exercise 4.4: Lagrange's identity for complex numbers". The Cauchy-Schwarz master class: an introduction to the art of mathematical inequalities. Cambridge University Press. pp. 68–69. ISBN 0-521-54677-X.
↑ Greene, Robert E.; Krantz, Steven G. (2002). Function Theory of One Complex Variable. Providence, R.I.: American Mathematical Society. p. 22, Exercise 16. ISBN 978-0-8218-2905-9.
↑ Palka, Bruce P. (1991). An Introduction to Complex Function Theory . Berlin, New York: Springer-Verlag. p. 27, Exercise 4.22. ISBN 978-0-387-97427-9..
↑ Howard Anton; Chris Rorres (2010). "Relationships between dot and cross products". Elementary Linear Algebra: Applications Version (10th ed.). John Wiley and Sons. p. 162. ISBN 978-0-470-43205-1.
↑ Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 94. ISBN 0-521-00551-5.
1 2 Door Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. ISBN 0-521-00551-5. See particularly § 7.4 Cross products in R⁷, p. 96.
↑ Jack B. Kuipers (2002). "§5.6 The norm". Quaternions and rotation sequences: a primer with applications to orbits. Princeton University Press. p. 111. ISBN 0-691-10298-8.
↑ See, for example, Frank Jones, Rice University, page 4 in Chapter 7 of a book still to be published.
↑ M. Fernández-Guasti, Alternative realization for the composition of relativistic velocities, Optics and Photonics 2011, vol. 8121 of The nature of light: What are photons? IV, pp. 812108–1–11. SPIE, 2011.

External links

Weisstein, Eric W. "Lagrange's Identity". MathWorld .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Weisstein-1] Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. ISBN 1-58488-347-2.

[Greene-2] Robert E Greene; Steven G Krantz (2006). "Exercise 16". Function theory of one complex variable (3rd ed.). American Mathematical Society. p. 22. ISBN 0-8218-3962-4.

[Boichenko-3] Vladimir A. Boichenko; Gennadiĭ Alekseevich Leonov; Volker Reitmann (2005). Dimension theory for ordinary differential equations. Vieweg+Teubner Verlag. p. 26. ISBN 3-519-00437-2.

[Steele-4] 1 2 3 J. Michael Steele (2004). "Exercise 4.4: Lagrange's identity for complex numbers". The Cauchy-Schwarz master class: an introduction to the art of mathematical inequalities. Cambridge University Press. pp. 68–69. ISBN 0-521-54677-X.

[5] Greene, Robert E.; Krantz, Steven G. (2002). Function Theory of One Complex Variable. Providence, R.I.: American Mathematical Society. p. 22, Exercise 16. ISBN 978-0-8218-2905-9.

[6] Palka, Bruce P. (1991). An Introduction to Complex Function Theory . Berlin, New York: Springer-Verlag. p. 27, Exercise 4.22. ISBN 978-0-387-97427-9..

[Anton-7] Howard Anton; Chris Rorres (2010). "Relationships between dot and cross products". Elementary Linear Algebra: Applications Version (10th ed.). John Wiley and Sons. p. 162. ISBN 978-0-470-43205-1.

[Lounesto1-8] Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 94. ISBN 0-521-00551-5.

[Lounesto-9] 1 2 Door Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. ISBN 0-521-00551-5. See particularly § 7.4 Cross products in R⁷, p. 96.

[Kuipers-10] Jack B. Kuipers (2002). "§5.6 The norm". Quaternions and rotation sequences: a primer with applications to orbits. Princeton University Press. p. 111. ISBN 0-691-10298-8.

[Jones-11] See, for example, Frank Jones, Rice University, page 4 in Chapter 7 of a book still to be published.

[12] M. Fernández-Guasti, Alternative realization for the composition of relativistic velocities, Optics and Photonics 2011, vol. 8121 of The nature of light: What are photons? IV, pp. 812108–1–11. SPIE, 2011.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]