
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x4 + 4.

In mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.
In number theory, a Liouville number is a real number x with the property that, for every positive integer n, there exists a pair of integers with q > 1 such that
In algebraic number theory, an algebraic integer is a complex number which is integral over the integers. That is, an algebraic integer is a complex root of some monic polynomial whose coefficients are integers. The set of all algebraic integers A is closed under addition, subtraction and multiplication and therefore is a commutative subring of the complex numbers.
In mathematics, an nth root of a number x is a number r which, when raised to the power n, yields x:

In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.
In mathematics, a quadratic irrational number is an irrational number that is the solution to some quadratic equation with rational coefficients which is irreducible over the rational numbers. Since fractions in the coefficients of a quadratic equation can be cleared by multiplying both sides by their least common denominator, a quadratic irrational is an irrational root of some quadratic equation with integer coefficients. The quadratic irrational numbers, a subset of the complex numbers, are algebraic numbers of degree 2, and can therefore be expressed as
In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.
In mathematics, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real algebraic integer greater than 1, all of whose Galois conjugates are less than 1 in absolute value. These numbers were discovered by Axel Thue in 1912 and rediscovered by G. H. Hardy in 1919 within the context of diophantine approximation. They became widely known after the publication of Charles Pisot's dissertation in 1938. They also occur in the uniqueness problem for Fourier series. Tirukkannapuram Vijayaraghavan and Raphael Salem continued their study in the 1940s. Salem numbers are a closely related set of numbers.
In mathematics, Roth's theorem is a fundamental result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that algebraic numbers cannot have many rational number approximations that are 'very good'. Over half a century, the meaning of very good here was refined by a number of mathematicians, starting with Joseph Liouville in 1844 and continuing with work of Axel Thue (1909), Carl Ludwig Siegel (1921), Freeman Dyson (1947), and Klaus Roth (1955).

Transcendental number theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.
In number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real numbers and , with , there exist integers and such that and
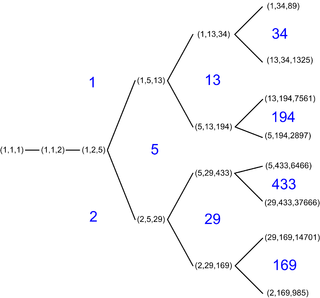
A Markov number or Markoff number is a positive integer x, y or z that is part of a solution to the Markov Diophantine equation
The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as:
In mathematics, specifically the area of Diophantine approximation, the Davenport–Schmidt theorem tells us how well a certain kind of real number can be approximated by another kind. Specifically it tells us that we can get a good approximation to irrational numbers that are not quadratic by using either quadratic irrationals or simply rational numbers. It is named after Harold Davenport and Wolfgang M. Schmidt.
In mathematics, the Markov spectrum devised by Andrey Markov is a complicated set of real numbers arising in Markov Diophantine equation and also in the theory of Diophantine approximation.

In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.
In number theory, Hurwitz's theorem, named after Adolf Hurwitz, gives a bound on a Diophantine approximation. The theorem states that for every irrational number ξ there are infinitely many relatively prime integers m, n such that
In number theory, specifically in Diophantine approximation theory, the Markov constant of an irrational number is the factor for which Dirichlet's approximation theorem can be improved for .








