
Approval voting is an electoral system in which voters can select any number of candidates instead of selecting only one.
The Condorcet paradox in social choice theory is a situation noted by the Marquis de Condorcet in the late 18th century, in which collective preferences can be cyclic, even if the preferences of individual voters are not cyclic. This is paradoxical, because it means that majority wishes can be in conflict with each other: Suppose majorities prefer, for example, candidate A over B, B over C, and yet C over A. When this occurs, it is because the conflicting majorities are each made up of different groups of individuals.

A Condorcet method is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, that is, a candidate preferred by more voters than any others, whenever there is such a candidate. A candidate with this property, the pairwise champion or beats-all winner, is formally called the Condorcet winner. The head-to-head elections need not be done separately; a voter's choice within any given pair can be determined from the ranking.
Arrow's impossibility theorem, the general possibility theorem or Arrow's paradox is an impossibility theorem in social choice theory that states that when voters have three or more distinct alternatives (options), no ranked voting electoral system can convert the ranked preferences of individuals into a community-wide ranking while also meeting the specified set of criteria: unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem is often cited in discussions of voting theory as it is further interpreted by the Gibbard–Satterthwaite theorem. The theorem is named after economist and Nobel laureate Kenneth Arrow, who demonstrated the theorem in his doctoral thesis and popularized it in his 1951 book Social Choice and Individual Values. The original paper was titled "A Difficulty in the Concept of Social Welfare".
The Smith set, also known as the top cycle, is a concept from the theory of electoral systems that generalizes the Condorcet winner to cases where no such winner exists, by allowing cycles of candidates to be treated jointly as if they were a single Condorcet winner. Named after John H. Smith, the Smith set consists the smallest non-empty set of candidates in a particular election, such that each member defeats every candidate outside the set in a pairwise election. The Smith set provides one standard of optimal choice for an election outcome. Voting systems that always elect a candidate from the Smith set pass the Smith criterion.
The independence of irrelevant alternatives (IIA), also known as binary independence or the independence axiom, is an axiom of decision theory and the social sciences that describes a necessary condition for rational behavior. The axiom says that adding "pointless" (rejected) options should not affect behavior. This is sometimes explained with a short story by philosopher Sidney Morgenbesser:
Morgenbesser, ordering dessert, is told by a waitress that he can choose between blueberry or apple pie. He orders apple. Soon the waitress comes back and explains cherry pie is also an option. Morgenbesser replies "In that case, I'll have blueberry."
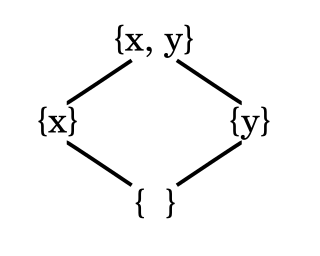
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
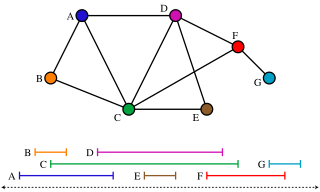
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.
Ranked pairs or the Tideman method is an electoral system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences. The ranked-pairs procedure can also be used to create a sorted list of winners.
The Schulze method is an electoral system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential dropping (SSD), cloneproof Schwartz sequential dropping (CSSD), the beatpath method, beatpath winner, path voting, and path winner. The Schulze method is a Condorcet method, which means that if there is a candidate who is preferred by a majority over every other candidate in pairwise comparisons, then this candidate will be the winner when the Schulze method is applied.
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent. Pairwise independent random variables with finite variance are uncorrelated.
The participation criterion, sometimes called join consistency, is a voting system criterion that says that a candidate should never lose an election because they have "too many supporters." In other words, adding a ballot that ranks A higher than B should not cause A to lose to B.
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a collective decision or social welfare in some sense. Whereas choice theory is concerned with individuals making choices based on their preferences, social choice theory is concerned with how to translate the preferences of individuals into the preferences of a group. A non-theoretical example of a collective decision is enacting a law or set of laws under a constitution. Another example is voting, where individual preferences over candidates are collected to elect a person that best represents the group's preferences.
In voting systems, the Minimax Condorcet method is a single-winner ranked-choice voting method that always elects the majority (Condorcet) winner. Minimax compares all candidates against each other in a round-robin tournament, then ranks candidates by their worst election result. The candidate with the largest (maximum) margin of victory in their worst (minimum) matchup is declared the winner.
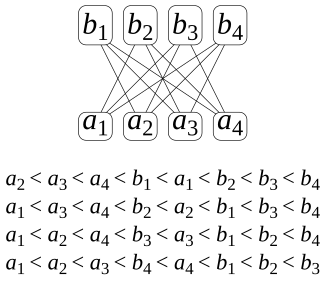
In mathematics, the dimension of a partially ordered set (poset) is the smallest number of total orders the intersection of which gives rise to the partial order. This concept is also sometimes called the order dimension or the Dushnik–Miller dimension of the partial order. Dushnik & Miller (1941) first studied order dimension; for a more detailed treatment of this subject than provided here, see Trotter (1992).
The Kemeny–Young method is an electoral system that uses ranked ballots and pairwise comparison counts to identify the most popular choices in an election. It is a Condorcet method because if there is a Condorcet winner, it will always be ranked as the most popular choice.
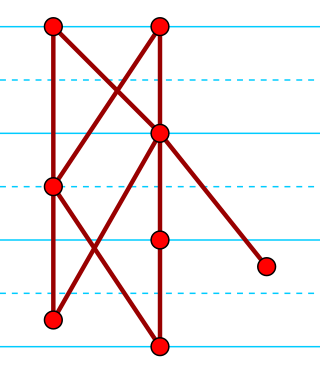
In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.
Maximal lotteries refers to a probabilistic voting system first considered by the French mathematician and social scientist Germain Kreweras in 1965. The method uses preferential ballots and returns so-called maximal lotteries, i.e., probability distributions over the alternatives that are weakly preferred to any other probability distribution. Maximal lotteries satisfy the Condorcet criterion, the Smith criterion, polynomial runtime, and probabilistic versions of reinforcement, participation, and independence of clones.

A tournament solution is a function that maps an oriented complete graph to a nonempty subset of its vertices. It can informally be thought of as a way to find the "best" alternatives among all of the alternatives that are "competing" against each other in the tournament. Tournament solutions originate from social choice theory, but have also been considered in sports competition, game theory, multi-criteria decision analysis, biology, webpage ranking, and dueling bandit problems.
Comparison of electoral systems is the result of comparative politics for electoral systems. Electoral systems are the rules for conducting elections, a main component of which is the algorithm for determining the winner from the ballots cast. This article discusses methods and results of comparing different electoral systems, both those that elect a unique candidate in a 'single-winner' election and those that elect a group of representatives in a multiwinner election.









