In mathematics, a leaky integrator equation is a specific differential equation, used to describe a component or system that takes the integral of an input, but gradually leaks a small amount of input over time. It appears commonly in hydraulics, electronics, and neuroscience where it can represent either a single neuron or a local population of neurons. [1]
The equation is of the form
where C is the input and A is the rate of the 'leak'.
The equation is a nonhomogeneous first-order linear differential equation. For constant C its solution is
where is a constant encoding the initial condition.
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:
The characteristic impedance or surge impedance (usually written Z0) of a uniform transmission line is the ratio of the amplitudes of voltage and current of a wave travelling in one direction along the line in the absence of reflections in the other direction. Equivalently, it can be defined as the input impedance of a transmission line when its length is infinite. Characteristic impedance is determined by the geometry and materials of the transmission line and, for a uniform line, is not dependent on its length. The SI unit of characteristic impedance is the ohm.
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter design. The filter is sometimes called a high-cut filter, or treble-cut filter in audio applications. A low-pass filter is the complement of a high-pass filter.
In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as for some scalar eigenvalue The solutions to this equation may also be subject to boundary conditions that limit the allowable eigenvalues and eigenfunctions.
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.
Hebbian theory is a neuropsychological theory claiming that an increase in synaptic efficacy arises from a presynaptic cell's repeated and persistent stimulation of a postsynaptic cell. It is an attempt to explain synaptic plasticity, the adaptation of brain neurons during the learning process. It was introduced by Donald Hebb in his 1949 book The Organization of Behavior. The theory is also called Hebb's rule, Hebb's postulate, and cell assembly theory. Hebb states it as follows:
Let us assume that the persistence or repetition of a reverberatory activity tends to induce lasting cellular changes that add to its stability. ... When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions.
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems.
A Hopfield network is a spin glass system used to model neural networks, based on Ernst Ising's work with Wilhelm Lenz on the Ising model of magnetic materials. Hopfield networks were first described with respect to recurrent neural networks independently by Kaoru Nakano in 1971 and Shun'ichi Amari in 1972, and with respect to biological neural networks by William Little in 1974, and were popularised by John Hopfield in 1982. Hopfield networks serve as content-addressable ("associative") memory systems with binary threshold nodes, or with continuous variables. Hopfield networks also provide a model for understanding human memory.
Nondimensionalization is the partial or full removal of physical dimensions from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis. In some physical systems, the term scaling is used interchangeably with nondimensionalization, in order to suggest that certain quantities are better measured relative to some appropriate unit. These units refer to quantities intrinsic to the system, rather than units such as SI units. Nondimensionalization is not the same as converting extensive quantities in an equation to intensive quantities, since the latter procedure results in variables that still carry units.
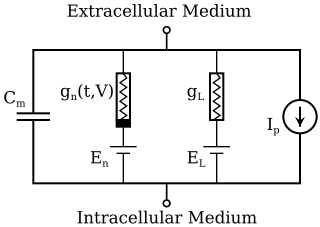
The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical engineering characteristics of excitable cells such as neurons and muscle cells. It is a continuous-time dynamical system.
In neuroscience, classical cable theory uses mathematical models to calculate the electric current along passive neurites, particularly the dendrites that receive synaptic inputs at different sites and times. Estimates are made by modeling dendrites and axons as cylinders composed of segments with capacitances and resistances combined in parallel. The capacitance of a neuronal fiber comes about because electrostatic forces are acting through the very thin lipid bilayer. The resistance in series along the fiber is due to the axoplasm's significant resistance to movement of electric charge.
A multi-compartment model is a type of mathematical model used for describing the way materials or energies are transmitted among the compartments of a system. Sometimes, the physical system that we try to model in equations is too complex, so it is much easier to discretize the problem and reduce the number of parameters. Each compartment is assumed to be a homogeneous entity within which the entities being modeled are equivalent. A multi-compartment model is classified as a lumped parameters model. Similar to more general mathematical models, multi-compartment models can treat variables as continuous, such as a differential equation, or as discrete, such as a Markov chain. Depending on the system being modeled, they can be treated as stochastic or deterministic.
Biological neuron models, also known as spiking neuron models, are mathematical descriptions of the conduction of electrical signals in neurons. Neurons are electrically excitable cells within the nervous system, able to fire electric signals, called action potentials, across a neural network. These mathematical models describe the role of the biophysical and geometrical characteristics of neurons on the conduction of electrical activity.
In physics and engineering, the time constant, usually denoted by the Greek letter τ (tau), is the parameter characterizing the response to a step input of a first-order, linear time-invariant (LTI) system. The time constant is the main characteristic unit of a first-order LTI system. It gives speed of the response.
In mathematics, the characteristic equation (or auxiliary equation) is an algebraic equation of degree n upon which depends the solution of a given nth-order differential equation or difference equation. The characteristic equation can only be formed when the differential or difference equation is linear and homogeneous, and has constant coefficients. Such a differential equation, with y as the dependent variable, superscript (n) denoting nth-derivative, and an, an − 1, ..., a1, a0 as constants,
The quadratic integrate and fire (QIF) model is a biological neuron model that describes action potentials in neurons. In contrast to physiologically accurate but computationally expensive neuron models like the Hodgkin–Huxley model, the QIF model seeks only to produce action potential-like patterns by ignoring the dynamics of transmembrane currents and ion channels. Thus, the QIF model is computationally efficient and has found ubiquitous use in computational neuroscience.
In mathematics, the exponential response formula (ERF), also known as exponential response and complex replacement, is a method used to find a particular solution of a non-homogeneous linear ordinary differential equation of any order. The exponential response formula is applicable to non-homogeneous linear ordinary differential equations with constant coefficients if the function is polynomial, sinusoidal, exponential or the combination of the three. The general solution of a non-homogeneous linear ordinary differential equation is a superposition of the general solution of the associated homogeneous ODE and a particular solution to the non-homogeneous ODE. Alternative methods for solving ordinary differential equations of higher order are method of undetermined coefficients and method of variation of parameters.
The spike response model (SRM) is a spiking neuron model in which spikes are generated by either a deterministic or a stochastic threshold process. In the SRM, the membrane voltage V is described as a linear sum of the postsynaptic potentials (PSPs) caused by spike arrivals to which the effects of refractoriness and adaptation are added. The threshold is either fixed or dynamic. In the latter case it increases after each spike. The SRM is flexible enough to account for a variety of neuronal firing pattern in response to step current input. The SRM has also been used in the theory of computation to quantify the capacity of spiking neural networks; and in the neurosciences to predict the subthreshold voltage and the firing times of cortical neurons during stimulation with a time-dependent current stimulation. The name Spike Response Model points to the property that the two important filters and of the model can be interpreted as the response of the membrane potential to an incoming spike (response kernel , the PSP) and to an outgoing spike (response kernel , also called refractory kernel). The SRM has been formulated in continuous time and in discrete time. The SRM can be viewed as a generalized linear model (GLM) or as an (integrated version of) a generalized integrate-and-fire model with adaptation.
{{cite book}}: CS1 maint: multiple names: authors list (link)  | This mathematical analysis–related article is a stub. You can help Wikipedia by expanding it. |
 | This applied mathematics-related article is a stub. You can help Wikipedia by expanding it. |