
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.

In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, as part of his list of 23 problems in mathematics.
In mathematics, Hausdorff measure is a generalization of the traditional notions of area and volume to non-integer dimensions, specifically fractals and their Hausdorff dimensions. It is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in or, more generally, in any metric space.

A Reuleaux triangle[ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.
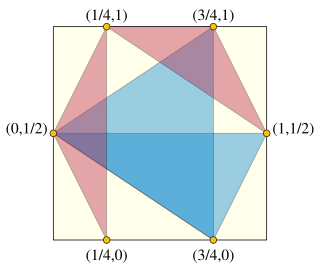
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.
A thrackle is an embedding of a graph in the plane, such that each edge is a Jordan arc and every pair of edges meet exactly once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, the crossing must be transverse.
In mathematics, the moving sofa problem or sofa problem is a two-dimensional idealisation of real-life furniture-moving problems and asks for the rigid two-dimensional shape of largest area that can be maneuvered through an L-shaped planar region with legs of unit width. The area thus obtained is referred to as the sofa constant. The exact value of the sofa constant is an open problem. The currently leading solution, by Joseph L. Gerver, has a value of approximately 2.2195 and is thought to be close to the optimal, based upon subsequent study and theoretical bounds.
The Blaschke selection theorem is a result in topology and convex geometry about sequences of convex sets. Specifically, given a sequence of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence and a convex set such that converges to in the Hausdorff metric. The theorem is named for Wilhelm Blaschke.

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
The covering problem of Rado is an unsolved problem in geometry concerning covering planar sets by squares. It was formulated in 1928 by Tibor Radó and has been generalized to more general shapes and higher dimensions by Richard Rado.

In combinatorial geometry, the Hadwiger conjecture states that any convex body in n-dimensional Euclidean space can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary if and only if the body is a parallelepiped. There also exists an equivalent formulation in terms of the number of floodlights needed to illuminate the body.
Moser's worm problem is an unsolved problem in geometry formulated by the Austrian-Canadian mathematician Leo Moser in 1966. The problem asks for the region of smallest area that can accommodate every plane curve of length 1. Here "accommodate" means that the curve may be rotated and translated to fit inside the region. In some variations of the problem, the region is restricted to be convex.
In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.
A geometric separator is a line that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset is small.











