
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid.

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". Another name for it is tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to e.g., pentagon. "Gon" being "angle" also is at the root of calling it quadrangle, 4-angle, in analogy to triangle. A quadrilateral with vertices , , and is sometimes denoted as .
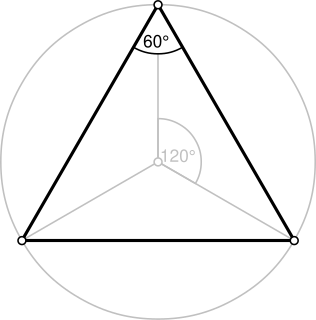
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, symmedians are three particular lines associated with every triangle. They are constructed by taking a median of the triangle, and reflecting the line over the corresponding angle bisector. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector.
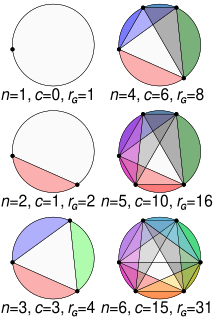
In geometry, the problem of dividing a circle into areas by means of an inscribed polygon with n sides in such a way as to maximise the number of areas created by the edges and diagonals, sometimes called Moser's circle problem, has a solution by an inductive method. The greatest possible number of regions, rG = + + 1, giving the sequence 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, .... Though the first five terms match the geometric progression 2n − 1, it diverges at n = 6, showing the risk of generalising from only a few observations.

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.
In geometry, lines in a plane or higher-dimensional space are said to be concurrent if they intersect at a single point. They are in contrast to parallel lines.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
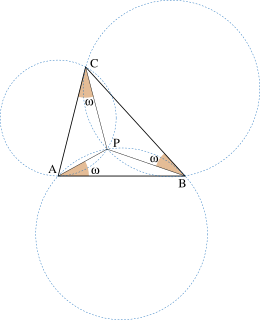
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
In triangle geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle, the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle and the Artzt parabolas which are parabolas touching two sidelines of the reference triangle at vertices of the triangle. The terminology of triangle conic is widely used in the literature without a formal definition,that is, without precisely formulating the relations a conic should have with the reference triangle so as to qualify it to be called a triangle conic (see,). WolframMathWorld has a page titled "Triangle conics" which gives a list of 42 items without giving a definition of triangle conic. However, Paris Pamfilos in his extensive collection of topics in geometry and topics in other fields related to geometry defines a triangle conic as a "conic circumscribing a triangle ABC or inscribed in a triangle ". The terminology triangle circle is used to denote a circle associated with the reference triangle is some way.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.























