
In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though it was first stated by Abraham de Moivre.

In mathematics, the error function is a special function (non-elementary) of sigmoid shape that occurs in probability, statistics, and partial differential equations describing diffusion. It is defined as:

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function defined by
In the physical sciences, the Airy functionAi(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals.
In mathematics, the Hamilton–Jacobi equation (HJE) is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations, and is a special case of the Hamilton–Jacobi–Bellman equation. It is named for William Rowan Hamilton and Carl Gustav Jacob Jacobi.

The Voigt profile is a probability distribution given by a convolution of a Cauchy-Lorentz distribution and a Gaussian distribution. It is often used in analyzing data from spectroscopy or diffraction.

In quantum field theory, the LSZ reduction formula is a method to calculate S-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann.
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. The symmetry algebra of a WZW model is an affine Lie algebra.
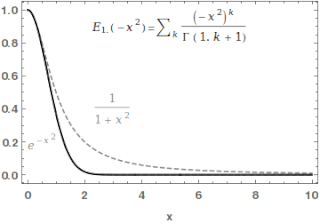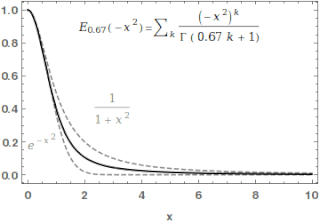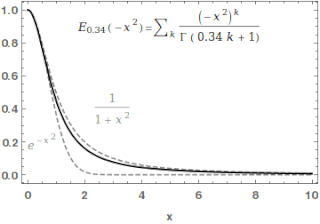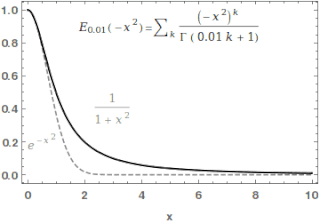
In mathematics, the Mittag-Leffler functionEα,β is a special function, a complex function which depends on two complex parameters α and β. It may be defined by the following series when the real part of α is strictly positive:

A premixed flame is a flame formed under certain conditions during the combustion of a premixed charge of fuel and oxidiser. Since the fuel and oxidiser—the key chemical reactants of combustion—are available throughout a homogeneous stoichiometric premixed charge, the combustion process once initiated sustains itself by way of its own heat release. The majority of the chemical transformation in such a combustion process occurs primarily in a thin interfacial region which separates the unburned and the burned gases. The premixed flame interface propagates through the mixture until the entire charge is depleted. The propagation speed of a premixed flame is known as the flame speed which depends on the convection-diffusion-reaction balance within the flame, i.e. on its inner chemical structure. The premixed flame is characterised as laminar or turbulent depending on the velocity distribution in the unburned pre-mixture.

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.

The Π pad is a specific type of attenuator circuit in electronics whereby the topology of the circuit is formed in the shape of the Greek letter "Π".
In mathematics, Maass forms or Maass wave forms are studied in the theory of automorphic forms. Maass forms are complex-valued smooth functions of the upper half plane, which transform in a similar way under the operation of a discrete subgroup of as modular forms. They are Eigenforms of the hyperbolic Laplace Operator defined on and satisfy certain growth conditions at the cusps of a fundamental domain of . In contrast to the modular forms the Maass forms need not be holomorphic. They were studied first by Hans Maass in 1949.
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.
A vortex sheet is a term used in fluid mechanics for a surface across which there is a discontinuity in fluid velocity, such as in slippage of one layer of fluid over another. While the tangential components of the flow velocity are discontinuous across the vortex sheet, the normal component of the flow velocity is continuous. The discontinuity in the tangential velocity means the flow has infinite vorticity on a vortex sheet.
In combustion, Burke–Schumann limit, or large Damköhler number limit, is the limit of infinitely fast chemistry, named after S.P. Burke and T.E.W. Schumann, due to their pioneering work on Burke–Schumann flame. One important conclusion of infinitely fast chemistry is the non-co-existence of fuel and oxidizer simultaneously except in a thin reaction sheet. The inner structure of the reaction sheet is described by Liñán's equation.
In the study of diffusion flame, Liñán's equation is a second-order nonlinear ordinary differential equation which describes the inner structure of the diffusion flame, first derived by Amable Liñán in 1974. The equation reads as


























