
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function f is a differentiable function F whose derivative is equal to the original function f. This can be stated symbolically as F' = f. The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as F and G.

In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration started as a method to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Today integration is used in a wide variety of scientific fields.
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions f, the Laplace transform is the integral
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of Göttingen in 1854, but not published in a journal until 1868. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration, or simulated using Monte Carlo Integration.

In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition of this integral was first published in 1894 by Stieltjes. It serves as an instructive and useful precursor of the Lebesgue integral, and an invaluable tool in unifying equivalent forms of statistical theorems that apply to discrete and continuous probability.
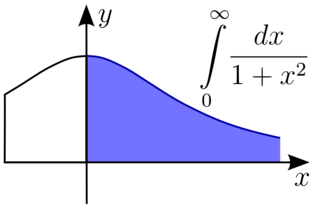
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which almost everywhere convergence of a sequence of functions implies convergence in the L1 norm. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over Riemann integration.
In mathematics, the Henstock–Kurzweil integral or generalized Riemann integral or gauge integral – also known as the (narrow) Denjoy integral, Luzin integral or Perron integral, but not to be confused with the more general wide Denjoy integral – is one of a number of inequivalent definitions of the integral of a function. It is a generalization of the Riemann integral, and in some situations is more general than the Lebesgue integral. In particular, a function is Lebesgue integrable if and only if the function and its absolute value are Henstock–Kurzweil integrable.
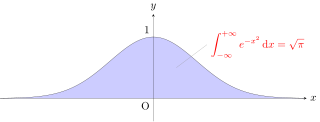
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
In mathematics, Laplace's method, named after Pierre-Simon Laplace, is a technique used to approximate integrals of the form

In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in (the real-number plane) are called double integrals, and integrals of a function of three variables over a region in (real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.
In complex analysis, Jordan's lemma is a result frequently used in conjunction with the residue theorem to evaluate contour integrals and improper integrals. The lemma is named after the French mathematician Camille Jordan.

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the X-axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.
In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.

Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.




































