Local inverse

The local inverse is a kind of inverse function or matrix inverse used in image and signal processing, as well as in other general areas of mathematics.

The concept of a local inverse came from interior reconstruction of CT^{[ clarification needed ]} images. One interior reconstruction method first approximately reconstructs the image outside the ROI (region of interest), and then subtracts the re-projection data of the image outside the ROI from the original projection data; then this data is used to make a new reconstruction. This idea can be widened to a full inverse. Instead of directly making an inverse, the unknowns outside of the local region can be inverted first. Recalculate the data from these unknowns (outside the local region), subtract this recalculated data from the original, and then take the inverse inside the local region using this newly produced data for the outside region.

This concept is a direct extension of the local tomography, generalized inverse and iterative refinement methods. It is used to solve the inverse problem with incomplete input data, similarly to local tomography. However this concept of local inverse can also be applied to complete input data.

Local inverse for full field of view system or over-determined system

${\displaystyle {\begin{bmatrix}f\\g\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}.}$

Assume there are ${\displaystyle E}$, ${\displaystyle F}$, ${\displaystyle G}$ and ${\displaystyle H}$ that satisfy

${\displaystyle {\begin{bmatrix}E&F\\G&H\end{bmatrix}}{\begin{bmatrix}A&B\\C&D\end{bmatrix}}=J.}$

Here ${\displaystyle J}$ is not equal to ${\displaystyle I}$, but ${\displaystyle J}$ is close to ${\displaystyle I}$, where ${\displaystyle I}$ is the identity matrix. Examples of matrices of the type ${\displaystyle {\begin{bmatrix}E&F\\G&H\end{bmatrix}}}$ are the filtered back-projection method for image reconstruction and the inverse with regularization. In this case the following is an approximate solution:

${\displaystyle {\begin{bmatrix}x_{0}\\y_{0}\end{bmatrix}}={\begin{bmatrix}E&F\\G&H\end{bmatrix}}{\begin{bmatrix}f\\g\end{bmatrix}}.}$

A better solution for ${\displaystyle x_{1}}$ can be found as follows:

${\displaystyle {\begin{bmatrix}x_{1}\\y_{1}\end{bmatrix}}={\begin{bmatrix}E&F\\G&H\end{bmatrix}}{\begin{bmatrix}f-By_{0}\\g-Dy_{0}\end{bmatrix}}.}$

In the above formula ${\displaystyle y_{1}}$ is useless, hence

${\displaystyle x_{1}=E(f-By_{0})+F(g-Dy_{0}).}$

In the same way, there is

${\displaystyle y_{1}=G(f-Ax_{0})+H(g-Cx_{0}).}$

In the above the solution is divided into two parts, ${\displaystyle x}$ inside the ROI and ${\displaystyle y}$ is outside the ROI, f inside of FOV(field of view) and g outside the FOV.

The two parts can be extended to many parts, in which case the extended method is referred to as the sub-region iterative refinement method ^[1]

Local inverse for limited-field-of-view system or under-determined system

${\displaystyle {\begin{bmatrix}f\\g\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}.}$

Assume ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, and ${\displaystyle D}$ are known matrices; ${\displaystyle x}$ and ${\displaystyle y}$ are unknown vectors; ${\displaystyle f}$ is a known vector; ${\displaystyle g}$ is an unknown vector. We are interested in determining x. What is a good solution?

Assume the inverse of the above matrix exists

${\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}{\begin{bmatrix}E&F\\G&H\end{bmatrix}}=J.}$

Here ${\displaystyle J}$ is or is close to ${\displaystyle I}$. The local inverse algorithm is as follows:

(1) ${\displaystyle g_{ex}}$. An extrapolated version of ${\displaystyle g}$ is obtained by

${\displaystyle g_{ex}|_{\partial G}=f|_{\partial F}.}$

(2) ${\displaystyle y_{0}}$. An approximate version of ${\displaystyle y}$ is calculated by

${\displaystyle y_{0}=Hg_{ex}.}$

(3) ${\displaystyle y'}$. A correction for ${\displaystyle y}$ is done by

${\displaystyle y'=y_{0}+y_{\text{co}}.}$

(4) ${\displaystyle f'}$. A corrected function for ${\displaystyle f}$ is calculated by

${\displaystyle f'=f-By'.}$

(5) ${\displaystyle g_{1ex}}$. An extrapolated function for ${\displaystyle g}$ is obtained by

${\displaystyle g_{1ex}|_{\partial G}=f'|_{\partial F}.}$

(6) ${\displaystyle x_{1}}$. A local inverse solution is obtained

${\displaystyle x_{1}=Ef'+Fg_{1ex}.}$

In the above algorithm, there are two time extrapolations for ${\displaystyle g}$ which are used to overcome the data truncation problem. There is a correction for ${\displaystyle y}$. This correction can be a constant correction to correct the DC values of ${\displaystyle y}$ or a linear correction according to prior knowledge about ${\displaystyle y}$. This algorithm can be found in the following reference:. ^[2]

In the example of the reference, ^[3] it is found that ${\displaystyle y'=y_{0}+y_{\text{co}}=ky_{0}}$, here ${\displaystyle k=1.04}$ the constant correction is made. A more complicated correction can be made, for example a linear correction, which might achieve better results.

A^+ B is close to 0

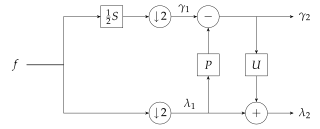
Shuang-ren Zhao defined a Local inverse ^[2] to solve the above problem. First consider the simplest solution

${\displaystyle f=Ax+By,}$

or

${\displaystyle Ax=f-By=f'.}$

Here ${\displaystyle f'=f-By}$ is the correct data in which there is no influence of the outside object function. From this data it is easy to get the correct solution,

${\displaystyle x'=A^{-1}f'.}$

Here ${\displaystyle x'}$ is a correct(or exact) solution for the unknown ${\displaystyle x}$, which means ${\displaystyle x'=x}$. In case that ${\displaystyle A}$ is not a square matrix or has no inverse, the generalized inverse can applied,

${\displaystyle x'=A^{+}(f-By)=A^{+}f'.}$

Since ${\displaystyle y}$ is unknown, if it is set to ${\displaystyle 0}$, an approximate solution is obtained.

${\displaystyle x_{0}=A^{+}f.}$

In the above solution the result ${\displaystyle x_{0}}$ is related to the unknown vector ${\displaystyle y}$. Since ${\displaystyle y}$ can have any value the result ${\displaystyle x_{0}}$ has very strong artifacts, namely

${\displaystyle \mathrm {error} _{0}=|x_{0}-x'|=|A^{+}By|}$.

These kind of artifacts are referred to as truncation artifacts in the field of CT image reconstruction. In order to minimize the above artifacts in the solution, a special matrix ${\displaystyle Q}$ is considered, which satisfies

${\displaystyle QB=0,}$

and thus satisfies

${\displaystyle QAx=Qf-QBy=Qf.}$

Solving the above equation with Generalized inverse gives

${\displaystyle x_{1}=[QA]^{+}Qf=[A]^{+}Q^{+}Qf.}$

Here ${\displaystyle Q^{+}}$ is the generalized inverse of ${\displaystyle Q}$, and ${\displaystyle x_{1}}$ is a solution for ${\displaystyle x}$. It is easy to find a matrix Q which satisfies ${\displaystyle QB=0}$, specifically ${\displaystyle Q}$ can be written as the following:

${\displaystyle Q=I-BB^{+}.}$

This matrix ${\displaystyle Q}$ is referred as the transverse projection of ${\displaystyle B}$, and ${\displaystyle B^{+}}$ is the generalized inverse of ${\displaystyle B}$. The matrix ${\displaystyle B^{+}}$ satisfies

${\displaystyle BB^{+}B=B,}$

from which it follows that

${\displaystyle QB=[I-BB^{+}]B=B-BB^{+}B=B-B=0.}$

It is easy to prove that ${\displaystyle QQ=Q}$:

${\displaystyle {\begin{aligned}QQ&=[I-BB^{+}][I-BB^{+}]=I-2BB^{+}+BB^{+}BB^{+}\\&=I-2BB^{+}+BB^{+}=I-BB^{+}=Q,\end{aligned}}}$

and hence

${\displaystyle QQQ=(QQ)Q=QQ=Q.}$

Hence Q is also the generalized inverse of Q

That means

${\displaystyle Q^{+}Q=QQ=Q.}$

Hence,

${\displaystyle x_{1}=A^{+}[Q]^{+}Qf=A^{+}Qf}$

or

${\displaystyle x_{1}=[A]^{+}[I-BB^{+}]f.}$

The matrix

${\displaystyle A^{L}=[A]^{+}[I-BB^{+}]}$

is referred to as the local inverse of the matrix ${\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}.}$ Using the local inverse instead of the generalized inverse or the inverse can avoid artifacts from unknown input data. Considering,

${\displaystyle [A]^{+}[I-BB^{+}]f'=[A]^{+}[I-BB^{+}](f-By)=[A]^{+}[I-BB^{+}]f.}$

Hence there is

${\displaystyle x_{1}=[A]^{+}[I-BB^{+}]f'.}$

Hence ${\displaystyle x_{1}}$ is only related to the correct data ${\displaystyle f'}$. This kind error can be calculated as

${\displaystyle \mathrm {error} _{1}=|x_{1}-x'|=|[A]^{+}BB^{+}f'|.}$

This kind error are called the bowl effect. The bowl effect is not related to the unknown object ${\displaystyle y}$, it is only related to the correct data ${\displaystyle f'}$.

In case the contribution of ${\displaystyle [A]^{+}BB^{+}f'}$ to ${\displaystyle x}$ is smaller than that of ${\displaystyle [A]^{+}By}$, or

${\displaystyle \mathrm {error} _{1}\ll \mathrm {error} _{0},}$

the local inverse solution ${\displaystyle x_{1}}$ is better than ${\displaystyle x_{0}}$ for this kind of inverse problem. Using ${\displaystyle x_{1}}$ instead of ${\displaystyle x_{0}}$, the truncation artifacts are replaced by the bowl effect. This result is the same as in local tomography, hence the local inverse is a direct extension of the concept of local tomography.

It is well known that the solution of the generalized inverse is a minimal L2 norm method. From the above derivation it is clear that the solution of the local inverse is a minimal L2 norm method subject to the condition that the influence of the unknown object ${\displaystyle y}$ is ${\displaystyle 0}$. Hence the local inverse is also a direct extension of the concept of the generalized inverse.

See also

• Formulation of the Jacobian conjecture
• Interior image reconstruction of CT scans
• interior reconstruction
• extrapolation
• matrix inverse
• generalized inverse
• iterative refinement
• Local tomography

References

1. Shuangren Zhao, Xintie Yang, Iterative reconstruction in all sub-regions, SCIENCEPAPER ONLINE. 2006; 1(4): page 301–308, http://www.paper.edu.cn/uploads/journal/2007/42/1673-7180(2006)04-0301-08.pdf
2. Shuangren Zhao, Kang Yang, Dazong Jiang, Xintie Yang, Interior reconstruction using local inverse, J Xray Sci Technol. 2011; 19(1): 69–90
3. S. Zhao, D Jaffray, Iterative reconstruction and reprojection for truncated projections, AAPM 2004, Abstract in Medical Physics 2004, Volume 31, P1719, http://imrecons.com/wp-content/uploads/2013/02/iterative_extro.pdf