
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equality. Any number is equal to itself (reflexive). If , then (symmetric). If and , then (transitive).

In mathematics, when the elements of some set have a notion of equivalence, then one may naturally split the set into equivalence classes. These equivalence classes are constructed so that elements and belong to the same equivalence class if, and only if, they are equivalent.
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
In logic and related fields such as mathematics and philosophy, "if and only if" is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional, and can be likened to the standard material conditional combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other, though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, P if and only if Q means that P is true whenever Q is true, and the only case in which P is true is if Q is also true, whereas in the case of P if Q, there could be other scenarios where P is true and Q is false.
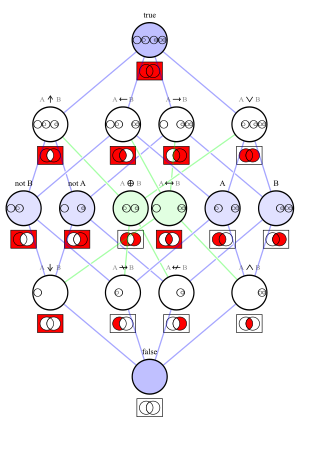
In logic, a logical connective is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives representing the truth functions of conjunction, disjunction, implication, biconditional, and negation. Some sources include other connectives, as in the table below.
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning.
In computer science, denotational semantics is an approach of formalizing the meanings of programming languages by constructing mathematical objects that describe the meanings of expressions from the languages. Other approaches providing formal semantics of programming languages include axiomatic semantics and operational semantics.
Operational semantics is a category of formal programming language semantics in which certain desired properties of a program, such as correctness, safety or security, are verified by constructing proofs from logical statements about its execution and procedures, rather than by attaching mathematical meanings to its terms. Operational semantics are classified in two categories: structural operational semantics formally describe how the individual steps of a computation take place in a computer-based system; by opposition natural semantics describe how the overall results of the executions are obtained. Other approaches to providing a formal semantics of programming languages include axiomatic semantics and denotational semantics.
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.
In programming language theory, semantics is the rigorous mathematical study of the meaning of programming languages. Semantics assigns computational meaning to valid strings in a programming language syntax. It is closely related to, and often crosses over with, the semantics of mathematical proofs.
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke.
In linguistics, focus is a grammatical category that conveys which part of the sentence contributes new, non-derivable, or contrastive information. In the English sentence "Mary only insulted BILL", focus is expressed prosodically by a pitch accent on "Bill" which identifies him as the only person Mary insulted. By contrast, in the sentence "Mary only INSULTED Bill", the verb "insult" is focused and thus expresses that Mary performed no other actions towards Bill. Focus is a cross-linguistic phenomenon and a major topic in linguistics. Research on focus spans numerous subfields including phonetics, syntax, semantics, pragmatics, and sociolinguistics.
In the mathematics of binary relations, the composition of relations is the forming of a new binary relation R; S from two given binary relations R and S. In the calculus of relations, the composition of relations is called relative multiplication, and its result is called a relative product. Function composition is the special case of composition of relations where all relations involved are functions.
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.
In logic and linguistics, an expression is syncategorematic if it lacks a denotation but can nonetheless affect the denotation of a larger expression which contains it. Syncategorematic expressions are contrasted with categorematic expressions, which have their own denotations.
Pregroup grammar (PG) is a grammar formalism intimately related to categorial grammars. Much like categorial grammar (CG), PG is a kind of type logical grammar. Unlike CG, however, PG does not have a distinguished function type. Rather, PG uses inverse types combined with its monoidal operation.
In formal semantics, the squiggle operator is an operator that constrains the occurrence of focus. In one common definition, the squiggle operator takes a syntactic argument and a discourse salient argument and introduces a presupposition that the ordinary semantic value of is either a subset or an element of the focus semantic value of . The squiggle was first introduced by Mats Rooth in 1992 as part of his treatment of focus within the framework of alternative semantics. It has become one of the standard tools in formal work on focus, playing a key role in accounts of contrastive focus, ellipsis, deaccenting, and question-answer congruence.
Logic programming is a programming paradigm that includes languages based on formal logic, including Datalog and Prolog. This article describes the syntax and semantics of the purely declarative subset of these languages. Confusingly, the name "logic programming" also refers to a specific programming language that roughly corresponds to the declarative subset of Prolog. Unfortunately, the term must be used in both senses in this article.
This is a glossary of logic. Logic is the study of the principles of valid reasoning and argumentation.










