Lucid (programming language)

Last updated
Lucid
Paradigm Dataflow
Designed by Edward A. Ashcroft
William W. Wadge
First appeared1976
Typing discipline Typeless
Major implementations
pLucid, GIPSY
Dialects
Granular Lucid, Indexical Lucid, Tensor Lucid, Forensic Lucid, Lucx, JOOIPL
Influenced by
ISWIM
Influenced
SISAL, PureData, Lustre

Lucid is a dataflow programming language designed to experiment with non-von Neumann programming models. It was designed by Bill Wadge and Ed Ashcroft and described in the 1985 book Lucid, the Dataflow Programming Language. [1]

Contents

pLucid was the first interpreter for Lucid.

Model

Lucid uses a demand-driven model for data computation. Each statement can be understood as an equation defining a network of processors and communication lines between them through which data flows. Each variable is an infinite stream of values and every function is a filter or a transformer. Iteration is simulated by 'current' values and 'fby' (read as 'followed by') operator allowing composition of streams.

Lucid is based on an algebra of histories, a history being an infinite sequence of data items. Operationally, a history can be thought of as a record of the changing values of a variable, history operations such as first and next can be understood in ways suggested by their names. Lucid was originally conceived as a disciplined, mathematically pure, single-assignment language, in which verification would be simplified. However, the dataflow interpretation has been an important influence on the direction in which Lucid has evolved.

Details

In Lucid (and other dataflow languages) an expression that contains a variable that has not yet been bound waits until the variable has been bound, before proceeding. An expression like x + y will wait until both x and y are bound before returning with the output of the expression. An important consequence of this is that explicit logic for updating related values is avoided, which results in substantial code reduction, compared to mainstream languages.

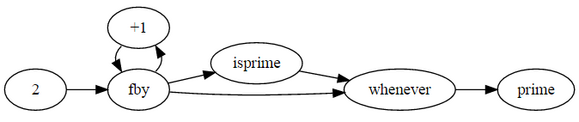
Each variable in Lucid is a stream of values. An expression n = 1 fby n + 1 defines a stream using the operator 'fby' (a mnemonic for "followed by"). fby defines what comes after the previous expression. (In this instance the stream produces 1,2,3,...). The values in a stream can be addressed by these operators (assuming x is the variable being used):

'first x' - fetches the first value in the stream x,

'x' - the current value of the stream,

'next x' - fetches the next value in the stream.

'asa' - an operator that does some thing 'as soon as' the condition given becomes true.

'x upon p' - upon is an operator that repeats the old value of the stream x, and updates to the new values only when the stream p makes a true value available. (It serves to slow down the stream x) i.e.: x upon p is the stream x with new values appearing upon the truth of p.

The computation is carried out by defining filters or transformation functions that act on these time-varying streams of data.

Examples

Factorial

facwheren=0fby(n+1);fac=1fby(fac*(n+1));end

Fibonacci sequence

fibwherefib=0fby(1fbyfib+nextfib);end

Total of a Sequence

totalwheretotal=0fbytotal+xend;

Running average

running_avgwheresum=first(input)fbysum+next(input);n=1fbyn+1;running_avg=sum/n;end;

Prime numbers

primewhereprime=2fby(nwhenever[[isprime]](n));n=3fbyn+1;isprime(n)=not(divs)asadivsorprime*prime>NwhereNiscurrentn;divs=Nmodprimeeq0;end;end

Dataflow diagram

Prime numbers sequence dataflow diagram (Lucid).png

Quick sort

qsort(a)=ifeof(firsta)then{{notatypo|a}}elsefollow(qsort(b0),qsort(b1))fiwherep=firsta<a;b0=awheneverp;b1=awhenevernotp;follow(x,y)=ifxdonethenyuponxdoneelsexfiwherexdone=iseodxfbyxdoneoriseodx;endend

Data flow diagram

     --------> whenever -----> qsort ---------     |             ^                           |     |             |                           |     |            not                          |     |             ^                           |     |---> first   |                           |     |       |     |                           |     |       V     |                           |     |---> less ---                            |     |             |                           |     |             V                           V  ---+--------> whenever -----> qsort -----> conc -------> ifthenelse ----->     |                                                       ^   ^     |                                                       |   |      --------> next ----> first ------> iseod --------------    |     |                                                           |      -----------------------------------------------------------

Root mean square

sqroot(avg(square(a)))wheresquare(x)=x*x;avg(y)=meanwheren=1fbyn+1;mean=firstyfbymean+d;d=(nexty-mean)/(n+1);end;sqroot(z)=approxasaerr<0.0001whereZiscurrentz;approx=Z/2fby(approx+Z/approx)/2;err=abs(square(approx)-Z);end;end

Hamming problem

hwhereh=1fbymerge(merge(2*h,3*h),5*h);merge(x,y)=ifxx<=yythenxxelseyyfiwherexx=xuponxx<=yy;yy=yuponyy<=xx;end;end;

Dataflow Diagram

Hamming problem dataflow diagram Hamming problem dataflow diagram (Lucid).png
Hamming problem dataflow diagram

References

  1. ↑ Wadge, William W.; Ashcroft, Edward A. (1985). Lucid, the Dataflow Programming Language . Academic Press. ISBN   0-12-729650-6 . Retrieved 8 January 2015.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.