The MacCullagh ellipsoid is defined by the equation:
where is the energy and are the components of the angular momentum, given in body's principal reference frame, with corresponding principal moments of inertia . The construction of such ellipsoid was conceived by James MacCullagh. [1]
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 to e = 1.
A sphere is a geometrical object in three-dimensional space that is the surface of a ball.
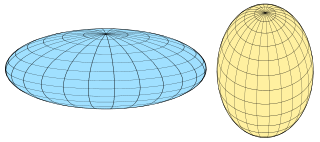
A spheroid, or ellipsoid of revolution, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.
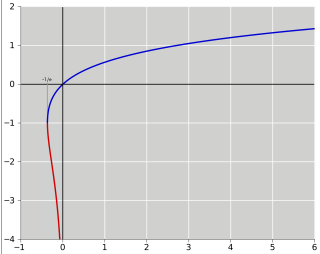
In mathematics, the Lambert W function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the inverse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function.
Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern. When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
The moment of inertia, otherwise known as the mass moment of inertia, angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis; similar to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation.
Physical geodesy is the study of the physical properties of the gravity field of the Earth, the geopotential, with a view to their application in geodesy.
In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.
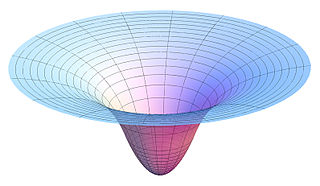
In classical mechanics, the gravitational potential at a location is equal to the work per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
Polarizability is the ability to form instantaneous dipoles. It is a property of matter. Polarizabilities determine the dynamical response of a bound system to external fields, and provide insight into a molecule's internal structure. In a solid, polarizability is defined as dipole moment per unit volume of the crystal cell.
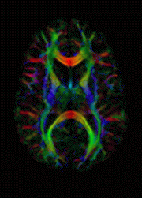
Diffusion-weighted magnetic resonance imaging is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast in MR images. It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not free, but reflects interactions with many obstacles, such as macromolecules, fibers, and membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain.
A homoeoid is a shell bounded by two concentric, similar ellipses or ellipsoids . When the thickness of the shell becomes negligible, it is called a thin homoeoid. The name homoeoid was coined by Lord Kelvin and Peter Tait.
Ellipsoidal coordinates are a three-dimensional orthogonal coordinate system that generalizes the two-dimensional elliptic coordinate system. Unlike most three-dimensional orthogonal coordinate systems that feature quadratic coordinate surfaces, the ellipsoidal coordinate system is based on confocal quadrics.
In physics, deformation is the continuum mechanics transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.
In geometry, a focaloid is a shell bounded by two concentric, confocal ellipses or ellipsoids (in 3D). When the thickness of the shell becomes negligible, it is called a thin focaloid.
A Jacobi ellipsoid is a triaxial ellipsoid under equilibrium which arises when a self-gravitating fluid body of uniform density rotates with a constant angular velocity. It is named after the German mathematician Carl Gustav Jacob Jacobi.
In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally. Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus and the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally.
In geometry a circular section is a circle on a quadric surface. It is a special plane section of the quadric, as this circle is the intersection with the quadric of the plane containing the circle.
