
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. The term potential energy was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to the ancient Greek philosopher Aristotle's concept of potentiality.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a given polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the reference plane (sometimes fundamental plane).

A magnetic field is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as or where is the Laplace operator, is the divergence operator, is the gradient operator, and is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function.

A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with magnetic north. Other methods may be used, including gyroscopes, magnetometers, and GPS receivers.

A galvanometer is an electromechanical measuring instrument for electric current. Early galvanometers were uncalibrated, but improved versions, called ammeters, were calibrated and could measure the flow of current more precisely. Galvanometers work by deflecting a pointer in response to an electric current flowing through a coil in a constant magnetic field. The mechanism is also used as an actuator in applications such as hard disks.

In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
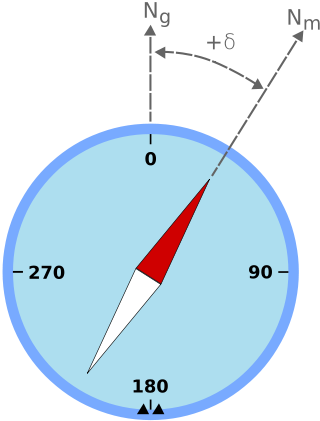
Magnetic declination is the angle between magnetic north and true north at a particular location on the Earth's surface. The angle can change over time due to polar wandering.

In mathematical physics, scalar potential describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.
In aviation, aircraft compass turns are turns made in an aircraft using only a magnetic compass for guidance.

In classical electromagnetism, magnetic vector potential is the vector quantity defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
In physics, the gyromagnetic ratio of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol γ, gamma. Its SI unit is the radian per second per tesla (rad⋅s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1).

Magnetostatics is the study of magnetic fields in systems where the currents are steady. It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that occur on time scales of nanoseconds or less. Magnetostatics is even a good approximation when the currents are not static – as long as the currents do not alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic storage devices as in computer memory.
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field B, takes the form:
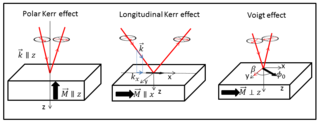
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.

The lateral earth pressure is the pressure that soil exerts in the horizontal direction. It is important because it affects the consolidation behavior and strength of the soil and because it is considered in the design of geotechnical engineering structures such as retaining walls, basements, tunnels, deep foundations and braced excavations.
Polar alignment is the act of aligning the rotational axis of a telescope's equatorial mount or a sundial's gnomon with a celestial pole to parallel Earth's axis.
The International Geomagnetic Reference Field (IGRF) is a standard mathematical description of the large-scale structure of the Earth's main magnetic field and its secular variation. It was created by fitting parameters of a mathematical model of the magnetic field to measured magnetic field data from surveys, observatories and satellites across the globe. The IGRF has been produced and updated under the direction of the International Association of Geomagnetism and Aeronomy (IAGA) since 1965.
In quantum mechanics, the Byers–Yang theorem states that all physical properties of a doubly connected system enclosing a magnetic flux through the opening are periodic in the flux with period . The theorem was first stated and proven by Nina Byers and Chen-Ning Yang (1961), and further developed by Felix Bloch (1970).



































