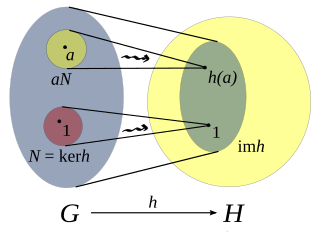
In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that
In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts.
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.

An exact sequence is a sequence of morphisms between objects such that the image of one morphism equals the kernel of the next.
In mathematics, a chain complex is an algebraic structure that consists of a sequence of abelian groups and a sequence of homomorphisms between consecutive groups such that the image of each homomorphism is included in the kernel of the next. Associated to a chain complex is its homology, which describes how the images are included in the kernels.

Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert.
In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces, known as their homology and cohomology groups. The result is due to two Austrian mathematicians, Walther Mayer and Leopold Vietoris. The method consists of splitting a space into subspaces, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection of the subspaces.
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
In algebra, a module homomorphism is a function between modules that preserves the module structures. Explicitly, if M and N are left modules over a ring R, then a function is called an R-module homomorphism or an R-linear map if for any x, y in M and r in R,
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes. The notion was introduced by Erich Kähler in the 1930s. It was adopted as standard in commutative algebra and algebraic geometry somewhat later, once the need was felt to adapt methods from calculus and geometry over the complex numbers to contexts where such methods are not available.
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before. In homotopy theory, for example, there are many examples of mappings that are invertible up to homotopy; and so large classes of homotopy equivalent spaces. Calculus of fractions is another name for working in a localized category.
In mathematics, the Ext functors are the derived functors of the Hom functor. Along with the Tor functor, Ext is one of the core concepts of homological algebra, in which ideas from algebraic topology are used to define invariants of algebraic structures. The cohomology of groups, Lie algebras, and associative algebras can all be defined in terms of Ext. The name comes from the fact that the first Ext group Ext1 classifies extensions of one module by another.
In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequences.
In mathematics, a triangulated category is a category with the additional structure of a "translation functor" and a class of "exact triangles". Prominent examples are the derived category of an abelian category, as well as the stable homotopy category. The exact triangles generalize the short exact sequences in an abelian category, as well as fiber sequences and cofiber sequences in topology.
In homological algebra in mathematics, the homotopy categoryK(A) of chain complexes in an additive category A is a framework for working with chain homotopies and homotopy equivalences. It lies intermediate between the category of chain complexes Kom(A) of A and the derived category D(A) of A when A is abelian; unlike the former it is a triangulated category, and unlike the latter its formation does not require that A is abelian. Philosophically, while D(A) turns into isomorphisms any maps of complexes that are quasi-isomorphisms in Kom(A), K(A) does so only for those that are quasi-isomorphisms for a "good reason", namely actually having an inverse up to homotopy equivalence. Thus, K(A) is more understandable than D(A).
In homological algebra, the hyperhomology or hypercohomology is a generalization of (co)homology functors which takes as input not objects in an abelian category but instead chain complexes of objects, so objects in . It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex since hypercohomology corresponds to the derived global sections functor .
In mathematics, specifically in category theory, an exact category is a category equipped with short exact sequences. The concept is due to Daniel Quillen and is designed to encapsulate the properties of short exact sequences in abelian categories without requiring that morphisms actually possess kernels and cokernels, which is necessary for the usual definition of such a sequence.
In algebraic geometry, a presheaf with transfers is, roughly, a presheaf that, like cohomology theory, comes with pushforwards, “transfer” maps. Precisely, it is, by definition, a contravariant additive functor from the category of finite correspondences to the category of abelian groups.
In mathematics, derived noncommutative algebraic geometry, the derived version of noncommutative algebraic geometry, is the geometric study of derived categories and related constructions of triangulated categories using categorical tools. Some basic examples include the bounded derived category of coherent sheaves on a smooth variety, , called its derived category, or the derived category of perfect complexes on an algebraic variety, denoted . For instance, the derived category of coherent sheaves on a smooth projective variety can be used as an invariant of the underlying variety for many cases. Unfortunately, studying derived categories as geometric objects of themselves does not have a standardized name.
In algebraic geometry, a mixed Hodge structure is an algebraic structure containing information about the cohomology of general algebraic varieties. It is a generalization of a Hodge structure, which is used to study smooth projective varieties.
































