In calculus, the chain rule is a formula to compute the derivative of a composite function. That is, if f and g are differentiable functions, then the chain rule expresses the derivative of their composite f∘g — the function which maps x to — in terms of the derivatives of f and g and the product of functions as follows:

The derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.
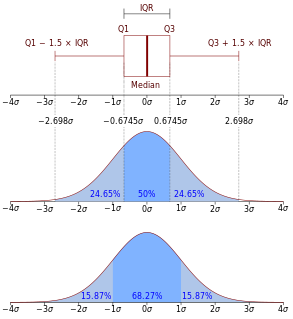
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.

Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether in 1915 and published in 1918, after a special case was proven by E. Cosserat and F. Cosserat in 1909. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries over physical space.

In physics and mathematics, the heat equation is a partial differential equation that describes how the distribution of some quantity evolves over time in a solid medium, as it spontaneously flows from places where it is higher towards places where it is lower. It is a special case of the diffusion equation.
In mathematics, Itô's lemma is an identity used in Itô calculus to find the differential of a time-dependent function of a stochastic process. It serves as the stochastic calculus counterpart of the chain rule. It can be heuristically derived by forming the Taylor series expansion of the function up to its second derivatives and retaining terms up to first order in the time increment and second order in the Wiener process increment. The lemma is widely employed in mathematical finance, and its best known application is in the derivation of the Black–Scholes equation for option values.
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated as

A thermodynamic potential is a scalar quantity used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a physical interpretation is the internal energy U. It is the energy of configuration of a given system of conservative forces and only has meaning with respect to a defined set of references. Expressions for all other thermodynamic energy potentials are derivable via Legendre transforms from an expression for U. In thermodynamics, external forces, such as gravity, are typically disregarded when formulating expressions for potentials. For example, while all the working fluid in a steam engine may have higher energy due to gravity while sitting on top of Mount Everest than it would at the bottom of the Mariana Trench, the gravitational potential energy term in the formula for the internal energy would usually be ignored because changes in gravitational potential within the engine during operation would be negligible. In a large system under even homogeneous external force, like the earth atmosphere under gravity, the intensive parameters should be studied locally having even in equilibrium different values in different places far from each other (see thermodynamic models of troposphere].
The path integral formulation of quantum mechanics is a description of quantum theory that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. It can be used to calculate the informational difference between measurements.
In statistics, propagation of uncertainty is the effect of variables' uncertainties on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations which propagate due to the combination of variables in the function.
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the derivative of the function.

Non-linear least squares is the form of least squares analysis used to fit a set of m observations with a model that is non-linear in n unknown parameters (m ≥ n). It is used in some forms of nonlinear regression. The basis of the method is to approximate the model by a linear one and to refine the parameters by successive iterations. There are many similarities to linear least squares, but also some significant differences. In economic theory, the non-linear least squares method is applied in (i) the probit regression, (ii) threshold regression, (iii) smooth regression, (iv) logistic link regression, (v) Box-Cox transformed regressors.

In mathematical finance, the Black–Scholes equation is a partial differential equation (PDE) governing the price evolution of a European call or European put under the Black–Scholes model. Broadly speaking, the term may refer to a similar PDE that can be derived for a variety of options, or more generally, derivatives.
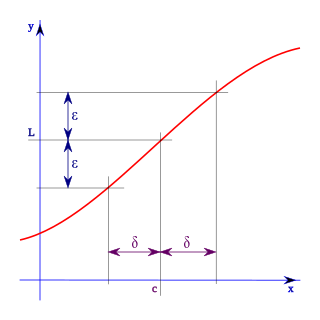
In calculus, the (ε, δ)-definition of limit is a formalization of the notion of limit. The concept is due to Augustin-Louis Cauchy, who never gave an definition of limit in his Cours d'Analyse, but occasionally used arguments in proofs. It was first given as a formal definition by Bernard Bolzano in 1817, and the definitive modern statement was ultimately provided by Karl Weierstrass. It makes rigorous the following informal notion: the dependent expression f(x) approaches the value L as the variable x approaches the value c if f(x) can be made as close as desired to L by taking x sufficiently close to c.
In mathematical physics, the Berezin integral, named after Felix Berezin,, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; the word "integral" is used because the Berezin integral has properties analogous to the Lebesgue integral and because it extends the path integral in physics, where it is used as a sum over histories for fermions.
In calculus, the differential represents the principal part of the change in a function y = f(x) with respect to changes in the independent variable. The differential dy is defined by
In mathematical analysis, and applications in geometry, applied mathematics, engineering, natural sciences, and economics, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The "input" variables take real values, while the "output", also called the "value of the function", may be real or complex. However, the study of the complex valued functions may be easily reduced to the study of the real valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real valued functions will be considered in this article.
Discrete calculus or the calculus of discrete functions, is the mathematical study of incremental change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. The word calculus is a Latin word, meaning originally "small pebble"; as such pebbles were used for calculation, the meaning of the word has evolved and today usually means a method of computation. Meanwhile, calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the study of continuous change.


























