Arrow's impossibility theorem, the general possibility theorem or Arrow's paradox is an impossibility theorem in social choice theory that states that when voters have three or more distinct alternatives (options), no ranked voting electoral system can convert the ranked preferences of individuals into a community-wide ranking while also meeting the specified set of criteria: unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem is often cited in discussions of voting theory as it is further interpreted by the Gibbard–Satterthwaite theorem. The theorem is named after economist and Nobel laureate Kenneth Arrow, who demonstrated the theorem in his doctoral thesis and popularized it in his 1951 book Social Choice and Individual Values. The original paper was titled "A Difficulty in the Concept of Social Welfare".
In social choice theory, the Gibbard–Satterthwaite theorem is a result published independently by philosopher Allan Gibbard in 1973 and economist Mark Satterthwaite in 1975. It deals with deterministic ordinal electoral systems that choose a single winner. It states that for every voting rule, one of the following three things must hold:
- The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or
- The rule limits the possible outcomes to two alternatives only; or
- The rule is susceptible to tactical voting: in certain conditions, a voter's sincere ballot may not best defend their opinion.
Ranked pairs or the Tideman method is an electoral system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences. The ranked-pairs procedure can also be used to create a sorted list of winners.
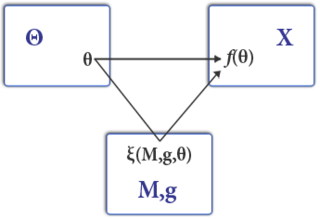
Mechanism design is a field in economics and game theory that takes an objectives-first approach to designing economic mechanisms or incentives, toward desired objectives, in strategic settings, where players act rationally. Because it starts at the end of the game, then goes backwards, it is also called reverse game theory. It has broad applications, from economics and politics in such fields as market design, auction theory and social choice theory to networked-systems.
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a collective decision or social welfare in some sense. Whereas choice theory is concerned with individuals making choices based on their preferences, social choice theory is concerned with how to translate the preferences of individuals into the preferences of a group. A non-theoretical example of a collective decision is enacting a law or set of laws under a constitution. Another example is voting, where individual preferences over candidates are collected to elect a person that best represents the group's preferences.
The revelation principle is a fundamental principle in mechanism design. It states that if a social choice function can be implemented by an arbitrary mechanism, then the same function can be implemented by an incentive-compatible-direct-mechanism with the same equilibrium outcome (payoffs).
Implementation theory is an area of research in game theory concerned with whether a class of mechanisms can be designed whose equilibrium outcomes implement a given set of normative goals or welfare criteria.
In social choice theory, a dictatorship mechanism is a rule by which, among all possible alternatives, the results of voting mirror a single pre-determined person's preferences, without consideration of the other voters. Dictatorship by itself is not considered a good mechanism in practice, but it is theoretically important: by Arrow's impossibility theorem, when there are at least three alternatives, dictatorship is the only ranked voting electoral system that satisfies unrestricted domain, Pareto efficiency, and independence of irrelevant alternatives. Similarly, by Gibbard's theorem, when there are at least three alternatives, dictatorship is the only strategyproof rule.
In cooperative game theory and social choice theory, the Nakamura number measures the degree of rationality of preference aggregation rules, such as voting rules. It is an indicator of the extent to which an aggregation rule can yield well-defined choices.
In social choice and operations research, the utilitarian rule is a rule saying that, among all possible alternatives, society should pick the alternative which maximizes the sum of the utilities of all individuals in society. It is a formal mathematical representation of the utilitarian philosophy.

Jean-François Mertens was a Belgian game theorist and mathematical economist.

Arunava Sen is a professor of economics at the Indian Statistical Institute. He works on Game Theory, Social Choice Theory, Mechanism Design, Voting and Auctions.
Maximal lotteries refers to a probabilistic voting system first considered by the French mathematician and social scientist Germain Kreweras in 1965. The method uses preferential ballots and returns so-called maximal lotteries, i.e., probability distributions over the alternatives that are weakly preferred to any other probability distribution. Maximal lotteries satisfy the Condorcet criterion, the Smith criterion, reversal symmetry, polynomial runtime, and probabilistic versions of reinforcement, participation, and independence of clones.
Proportional approval voting (PAV) is a proportional electoral system for selecting committees. It is an extension of the D'Hondt method of apportionment that additionally allows for personal votes (voters vote for candidates, not for a party list). The voters vote via approval ballots where each voter marks those candidates that the voter finds acceptable.
Efficiency and fairness are two major goals of welfare economics. Given a set of resources and a set of agents, the goal is to divide the resources among the agents in a way that is both Pareto efficient (PE) and envy-free (EF). The goal was first defined by David Schmeidler and Menahem Yaari. Later, the existence of such allocations has been proved under various conditions.
In mechanism design, monotonicity is a property of a social choice function. It is a necessary condition for being able to implement the function using a strategyproof mechanism. Its verbal description is:
If changing one agent's type changes the outcome under the social choice function, then the resulting difference in utilities of the new and original outcomes evaluated at the new type of this agent must be at least as much as this difference in utilities evaluated at the original type of this agent.
Resource monotonicity is a principle of fair division. It says that, if there are more resources to share, then all agents should be weakly better off; no agent should lose from the increase in resources. The RM principle has been studied in various division problems.
Impartial culture (IC) or the culture of indifference is a probabilistic model used in social choice theory for analyzing ranked voting method rules.
A jury theorem is a mathematical theorem proving that, under certain assumptions, a decision attained using majority voting in a large group is more likely to be correct than a decision attained by a single expert. It serves as a formal argument for the idea of wisdom of the crowd, for decision of questions of fact by jury trial, and for democracy in general.
Fractional approval voting is an electoral system using approval ballots, in which the outcome is fractional: for each alternative j there is a fraction pj between 0 and 1, such that the sum of pj is 1. It can be seen as a generalization of approval voting: in the latter, one candidate wins and the other candidates lose. The fractions pj can be interpreted in various ways, depending on the setting. Examples are:





