Matsubara frequency

In thermal quantum field theory, the Matsubara frequency summation (named after Takeo Matsubara) is a technique used to simplify calculations involving Euclidean (imaginary time) path integrals. ^[1]

In thermal quantum field theory, bosonic and fermionic quantum fields ${\displaystyle \phi (\tau )}$ are respectively periodic or antiperiodic in imaginary time ${\displaystyle \tau }$, with periodicity ${\displaystyle \beta =\hbar /k_{\rm {B}}T}$. Matsubara summation refers to the technique of expanding these fields in Fourier series

${\displaystyle \phi (\tau )={\frac {1}{\sqrt {\beta }}}\sum _{n}e^{-i\omega _{n}\tau }\phi (i\omega _{n})\Leftrightarrow \phi (i\omega _{n})={\frac {1}{\sqrt {\beta }}}\int _{0}^{\beta }d\tau \ e^{i\omega _{n}\tau }\phi (\tau ).}$

The frequencies ${\displaystyle \omega _{n}}$ are called the Matsubara frequencies, taking values from either of the following sets (with ${\displaystyle n\in \mathbb {Z} }$):

bosonic frequencies: ${\displaystyle \omega _{n}={\frac {2n\pi }{\beta }},}$

fermionic frequencies: ${\displaystyle \omega _{n}={\frac {(2n+1)\pi }{\beta }},}$

which respectively enforce periodic and antiperiodic boundary conditions on the field ${\displaystyle \phi (\tau )}$.

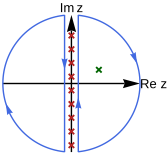
Once such substitutions have been made, certain diagrams contributing to the action take the form of a so-called Matsubara summation

${\displaystyle S_{\eta }={\frac {1}{\beta }}\sum _{i\omega _{n}}g(i\omega _{n}).}$

The summation will converge if ${\displaystyle g(z=i\omega )}$ tends to 0 in ${\displaystyle z\to \infty }$ limit in a manner faster than ${\displaystyle z^{-1}}$. The summation over bosonic frequencies is denoted as ${\displaystyle S_{\rm {B}}}$ (with ${\displaystyle \eta =+1}$), while that over fermionic frequencies is denoted as ${\displaystyle S_{\rm {F}}}$ (with ${\displaystyle \eta =-1}$). ${\displaystyle \eta }$ is the statistical sign.

In addition to thermal quantum field theory, the Matsubara frequency summation method also plays an essential role in the diagrammatic approach to solid-state physics, namely, if one considers the diagrams at finite temperature. ^{[2] [3] [4]}

Generally speaking, if at ${\displaystyle T=0\,{\text{K}}}$, a certain Feynman diagram is represented by an integral ${\displaystyle \int _{T=0}\mathrm {d} \omega \ g(\omega )}$, at finite temperature it is given by the sum ${\displaystyle S_{\eta }}$.

Summation formalism

General formalism

Figure 1.

Figure 2.

The trick to evaluate Matsubara frequency summation is to use a Matsubara weighting function h_η(z) that has simple poles located exactly at ${\displaystyle z=i\omega _{n}}$. ^[4] The weighting functions in the boson case η = +1 and fermion case η = −1 differ. The choice of weighting function will be discussed later. With the weighting function, the summation can be replaced by a contour integral surrounding the imaginary axis.

${\displaystyle S_{\eta }={\frac {1}{\beta }}\sum _{i\omega }g(i\omega )={\frac {1}{2\pi i\beta }}\oint g(z)h_{\eta }(z)\,dz,}$

As in Fig. 1, the weighting function generates poles (red crosses) on the imaginary axis. The contour integral picks up the residue of these poles, which is equivalent to the summation. This procedure is sometimes called Sommerfeld-Watson transformation. ^[5]

By deformation of the contour lines to enclose the poles of g(z) (the green cross in Fig. 2), the summation can be formally accomplished by summing the residue of g(z)h_η(z) over all poles of g(z),

${\displaystyle S_{\eta }=-{\frac {1}{\beta }}\sum _{z_{0}\in g(z){\text{ poles}}}\operatorname {Res} g(z_{0})h_{\eta }(z_{0}).}$

Note that a minus sign is produced, because the contour is deformed to enclose the poles in the clockwise direction, resulting in the negative residue.

Choice of Matsubara weighting function

To produce simple poles on boson frequencies ${\displaystyle z=i\omega _{n}}$, either of the following two types of Matsubara weighting functions can be chosen

${\displaystyle h_{\rm {B}}^{(1)}(z)={\frac {\beta }{1-e^{-\beta z}}}=-\beta n_{\rm {B}}(-z)=\beta (1+n_{\rm {B}}(z)),}$

${\displaystyle h_{\rm {B}}^{(2)}(z)={\frac {-\beta }{1-e^{\beta z}}}=\beta n_{\rm {B}}(z),}$

depending on which half plane the convergence is to be controlled in. ${\displaystyle h_{\rm {B}}^{(1)}(z)}$ controls the convergence in the left half plane (Re z < 0), while ${\displaystyle h_{\rm {B}}^{(2)}(z)}$ controls the convergence in the right half plane (Re z > 0). Here ${\displaystyle n_{\rm {B}}(z)=(e^{\beta z}-1)^{-1}}$ is the Bose–Einstein distribution function.

The case is similar for fermion frequencies. There are also two types of Matsubara weighting functions that produce simple poles at ${\displaystyle z=i\omega _{m}}$

${\displaystyle h_{\rm {F}}^{(1)}(z)={\frac {\beta }{1+e^{-\beta z}}}=\beta n_{\rm {F}}(-z)=\beta (1-n_{\rm {F}}(z)),}$

${\displaystyle h_{\rm {F}}^{(2)}(z)={\frac {-\beta }{1+e^{\beta z}}}=-\beta n_{\rm {F}}(z).}$

${\displaystyle h_{\rm {F}}^{(1)}(z)}$ controls the convergence in the left half plane (Re z < 0), while ${\displaystyle h_{\rm {F}}^{(2)}(z)}$ controls the convergence in the right half plane (Re z > 0). Here ${\displaystyle n_{\rm {F}}(z)=(e^{\beta z}+1)^{-1}}$ is the Fermi–Dirac distribution function.

In the application to Green's function calculation, g(z) always have the structure

${\displaystyle g(z)=G(z)e^{-z\tau },}$

which diverges in the left half plane given 0 < τ < β. So as to control the convergence, the weighting function of the first type is always chosen ${\displaystyle h_{\eta }(z)=h_{\eta }^{(1)}(z)}$. However, there is no need to control the convergence if the Matsubara summation does not diverge. In that case, any choice of the Matsubara weighting function will lead to identical results.

Table of Matsubara frequency summations

The following table contains ${\displaystyle S_{\eta }={\frac {1}{\beta }}\sum _{i\omega }g(i\omega )}$ for some simple rational functions g(z). The symbol η = ±1 is the statistical sign, +1 for bosons and -1 for fermions.

${\displaystyle g(i\omega )}$	${\displaystyle S_{\eta }}$
${\displaystyle (i\omega -\xi )^{-1}}$	${\displaystyle -\eta n_{\eta }(\xi )}$[1]
${\displaystyle (i\omega -\xi )^{-2}}$	${\displaystyle -\eta n_{\eta }^{\prime }(\xi )=\beta n_{\eta }(\xi )(\eta +n_{\eta }(\xi ))}$
${\displaystyle (i\omega -\xi )^{-n}}$	${\displaystyle -{\frac {\eta }{(n-1)!}}\partial _{\xi }^{n-1}n_{\eta }(\xi )}$
${\displaystyle {\frac {1}{(i\omega -\xi _{1})(i\omega -\xi _{2})}}}$	${\displaystyle -{\frac {\eta (n_{\eta }(\xi _{1})-n_{\eta }(\xi _{2}))}{\xi _{1}-\xi _{2}}}}$
${\displaystyle {\frac {1}{(i\omega -\xi _{1})^{2}(i\omega -\xi _{2})^{2}}}}$	${\displaystyle {\frac {\eta }{(\xi _{1}-\xi _{2})^{2}}}\left({\frac {2(n_{\eta }(\xi _{1})-n_{\eta }(\xi _{2}))}{\xi _{1}-\xi _{2}}}-(n_{\eta }^{\prime }(\xi _{1})+n_{\eta }^{\prime }(\xi _{2}))\right)}$
${\displaystyle {\frac {1}{(i\omega -\xi _{1})^{2}-\xi _{2}^{2}}}}$	${\displaystyle \eta c_{\eta }(\xi _{1},\xi _{2})\equiv -\eta {\frac {n_{\eta }(\xi _{1}+\xi _{2})-n_{\eta }(\xi _{1}-\xi _{2})}{2\xi _{2}}}}$
${\displaystyle {\frac {1}{(i\omega )^{2}-\xi ^{2}}}}$	${\displaystyle \eta c_{\eta }(0,\xi )=-{\frac {1}{2\xi }}(1+2\eta n_{\eta }(\xi ))}$
${\displaystyle {\frac {(i\omega )^{2}}{(i\omega )^{2}-\xi ^{2}}}}$	${\displaystyle -{\frac {\xi }{2}}(1+2\eta n_{\eta }(\xi ))}$[1]
${\displaystyle {\frac {1}{((i\omega )^{2}-\xi ^{2})^{2}}}}$	${\displaystyle -{\frac {\eta }{2\xi ^{2}}}(c_{\eta }(0,\xi )+n_{\eta }^{\prime }(\xi ))}$
${\displaystyle {\frac {(i\omega )^{2}}{((i\omega )^{2}-\xi ^{2})^{2}}}}$	${\displaystyle {\frac {\eta }{2}}(c_{\eta }(0,\xi )-n_{\eta }^{\prime }(\xi ))}$
${\displaystyle {\frac {(i\omega )^{2}+\xi ^{2}}{((i\omega )^{2}-\xi ^{2})^{2}}}}$	${\displaystyle -\eta n_{\eta }^{\prime }(\xi )=\beta n_{\eta }(\xi )(\eta +n_{\eta }(\xi ))}$
${\displaystyle {\frac {1}{((i\omega )^{2}-\xi _{1}^{2})((i\omega )^{2}-\xi _{2}^{2})}}}$	${\displaystyle {\frac {\eta (c_{\eta }(0,\xi _{1})-c_{\eta }(0,\xi _{2}))}{\xi _{1}^{2}-\xi _{2}^{2}}}}$
${\displaystyle \left({\frac {1}{(i\omega )^{2}-\xi _{1}^{2}}}+{\frac {1}{(i\omega )^{2}-\xi _{2}^{2}}}\right)^{2}}$	${\displaystyle \eta \left({\frac {3\xi _{1}^{2}+\xi _{2}^{2}}{2\xi _{1}^{2}(\xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta }^{\prime }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)}$[2]
${\displaystyle \left({\frac {1}{(i\omega )^{2}-\xi _{1}^{2}}}-{\frac {1}{(i\omega )^{2}-\xi _{2}^{2}}}\right)^{2}}$	${\displaystyle \eta \left(-{\frac {5\xi _{1}^{2}-\xi _{2}^{2}}{2\xi _{1}^{2}(\xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta }^{\prime }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)}$[2]

[1] Since the summation does not converge, the result may differ upon different choice of the Matsubara weighting function.

[2] (1 ↔ 2) denotes the same expression as the before but with index 1 and 2 interchanged.

Applications in physics

Zero temperature limit

In this limit ${\displaystyle \beta \rightarrow \infty }$, the Matsubara frequency summation is equivalent to the integration of imaginary frequency over imaginary axis.

${\displaystyle {\frac {1}{\beta }}\sum _{i\omega }=\int _{-i\infty }^{i\infty }{\frac {\mathrm {d} (i\omega )}{2\pi i}}.}$

Some of the integrals do not converge. They should be regularized by introducing the frequency cutoff ${\displaystyle \Omega }$, and then subtracting the divergent part (${\displaystyle \Omega }$-dependent) from the integral before taking the limit of ${\displaystyle \Omega \rightarrow \infty }$. For example, the free energy is obtained by the integral of logarithm,

${\displaystyle \eta \lim _{\Omega \rightarrow \infty }\left[\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi i}}\left(\ln(-i\omega +\xi )-{\frac {\pi \xi }{2\Omega }}\right)-{\frac {\Omega }{\pi }}(\ln \Omega -1)\right]=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta \xi &\xi <0,\end{array}}\right.}$

meaning that at zero temperature, the free energy simply relates to the internal energy below the chemical potential. Also the distribution function is obtained by the following integral

${\displaystyle \eta \lim _{\Omega \rightarrow \infty }\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi i}}\left({\frac {1}{-i\omega +\xi }}-{\frac {\pi }{2\Omega }}\right)=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta &\xi <0,\end{array}}\right.}$

which shows step function behavior at zero temperature.

Green's function related

Time domain

Consider a function G(τ) defined on the imaginary time interval (0,β). It can be given in terms of Fourier series,

${\displaystyle G(\tau )={\frac {1}{\beta }}\sum _{i\omega }G(i\omega )e^{-i\omega \tau },}$

where the frequency only takes discrete values spaced by 2π/β.

The particular choice of frequency depends on the boundary condition of the function G(τ). In physics, G(τ) stands for the imaginary time representation of Green's function

${\displaystyle G(\tau )=-\langle {\mathcal {T}}_{\tau }\psi (\tau )\psi ^{*}(0)\rangle .}$

It satisfies the periodic boundary condition G(τ+β)=G(τ) for a boson field. While for a fermion field the boundary condition is anti-periodic G(τ + β) = −G(τ).

Given the Green's function G(iω) in the frequency domain, its imaginary time representation G(τ) can be evaluated by Matsubara frequency summation. Depending on the boson or fermion frequencies that is to be summed over, the resulting G(τ) can be different. To distinguish, define

${\displaystyle G_{\eta }(\tau )={\begin{cases}G_{\rm {B}}(\tau ),&{\text{if }}\eta =+1,\\G_{\rm {F}}(\tau ),&{\text{if }}\eta =-1,\end{cases}}}$

with

${\displaystyle G_{\rm {B}}(\tau )={\frac {1}{\beta }}\sum _{i\omega _{n}}G(i\omega _{n})e^{-i\omega _{n}\tau },}$

${\displaystyle G_{\rm {F}}(\tau )={\frac {1}{\beta }}\sum _{i\omega _{m}}G(i\omega _{m})e^{-i\omega _{m}\tau }.}$

Note that τ is restricted in the principal interval (0,β). The boundary condition can be used to extend G(τ) out of the principal interval. Some frequently used results are concluded in the following table.

${\displaystyle G(i\omega )}$	${\displaystyle G_{\eta }(\tau )}$
${\displaystyle (i\omega -\xi )^{-1}}$	${\displaystyle -e^{\xi (\beta -\tau )}n_{\eta }(\xi )}$
${\displaystyle (i\omega -\xi )^{-2}}$	${\displaystyle e^{\xi (\beta -\tau )}n_{\eta }(\xi )\left(\tau +\eta \beta n_{\eta }(\xi )\right)}$
${\displaystyle (i\omega -\xi )^{-3}}$	${\displaystyle -{\frac {1}{2}}e^{\xi (\beta -\tau )}n_{\eta }(\xi )\left(\tau ^{2}+\eta \beta (\beta +2\tau )n_{\eta }(\xi )+2\beta ^{2}n_{\eta }^{2}(\xi )\right)}$
${\displaystyle (i\omega -\xi _{1})^{-1}(i\omega -\xi _{2})^{-1}}$	${\displaystyle -{\frac {e^{\xi _{1}(\beta -\tau )}n_{\eta }(\xi _{1})-e^{\xi _{2}(\beta -\tau )}n_{\eta }(\xi _{2})}{\xi _{1}-\xi _{2}}}}$
${\displaystyle (\omega ^{2}+m^{2})^{-1}}$	${\displaystyle {\frac {e^{-m\tau }}{2m}}+{\frac {\eta }{m}}\cosh {m\tau }\;n_{\eta }(m)}$
${\displaystyle i\omega (\omega ^{2}+m^{2})^{-1}}$	${\displaystyle {\frac {e^{-m\tau }}{2}}-\eta \,\sinh {m\tau }\;n_{\eta }(m)}$

Operator switching effect

The small imaginary time plays a critical role here. The order of the operators will change if the small imaginary time changes sign.

${\displaystyle \langle \psi \psi ^{*}\rangle =\langle {\mathcal {T}}_{\tau }\psi (\tau =0^{+})\psi ^{*}(0)\rangle =-G_{\eta }(\tau =0^{+})=-{\frac {1}{\beta }}\sum _{i\omega }G(i\omega )e^{-i\omega 0^{+}}}$

${\displaystyle \langle \psi ^{*}\psi \rangle =\eta \langle {\mathcal {T}}_{\tau }\psi (\tau =0^{-})\psi ^{*}(0)\rangle =-\eta G_{\eta }(\tau =0^{-})=-{\frac {\eta }{\beta }}\sum _{i\omega }G(i\omega )e^{i\omega 0^{+}}}$

Distribution function

The evaluation of distribution function becomes tricky because of the discontinuity of Green's function G(τ) at τ = 0. To evaluate the summation

${\displaystyle G(0)=\sum _{i\omega }(i\omega -\xi )^{-1},}$

both choices of the weighting function are acceptable, but the results are different. This can be understood if we push G(τ) away from τ = 0 a little bit, then to control the convergence, we must take ${\displaystyle h_{\eta }^{(1)}(z)}$ as the weighting function for ${\displaystyle G(\tau =0^{+})}$, and ${\displaystyle h_{\eta }^{(2)}(z)}$ for ${\displaystyle G(\tau =0^{-})}$.

Bosons

${\displaystyle G_{\rm {B}}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-n_{\rm {B}}(\xi ),}$

${\displaystyle G_{\rm {B}}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{-i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-(n_{\rm {B}}(\xi )+1).}$

Fermions

${\displaystyle G_{\rm {F}}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=n_{\rm {F}}(\xi ),}$

${\displaystyle G_{\rm {F}}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{-i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=n_{\rm {F}}(\xi )-1.}$

Free energy

Bosons

${\displaystyle {\frac {1}{\beta }}\sum _{i\omega _{n}}\ln(\beta (-i\omega _{n}+\xi ))={\frac {1}{\beta }}\ln(1-e^{-\beta \xi }),}$

Fermions

${\displaystyle -{\frac {1}{\beta }}\sum _{i\omega _{m}}\ln(\beta (-i\omega _{m}+\xi ))=-{\frac {1}{\beta }}\ln(1+e^{-\beta \xi }).}$

Diagram evaluations

Frequently encountered diagrams are evaluated here with the single mode setting. Multiple mode problems can be approached by a spectral function integral. Here ${\displaystyle \omega _{m}}$ is a fermionic Matsubara frequency, while ${\displaystyle \omega _{n}}$ is a bosonic Matsubara frequency.

Fermion self energy

${\displaystyle \Sigma (i\omega _{m})=-{\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{n}-\Omega }}={\frac {n_{\rm {F}}(\varepsilon )+n_{\rm {B}}(\Omega )}{i\omega _{m}-\varepsilon +\Omega }}.}$

Particle-hole bubble

${\displaystyle \Pi (i\omega _{n})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{m}-\varepsilon '}}=-{\frac {n_{\rm {F}}(\varepsilon )-n_{\rm {F}}\left(\varepsilon '\right)}{i\omega _{n}-\varepsilon +\varepsilon '}}.}$

Particle-particle bubble

${\displaystyle \Pi (i\omega _{n})=-{\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{-i\omega _{m}-\varepsilon '}}={\frac {1-n_{\rm {F}}\left(\varepsilon '\right)-n_{\rm {F}}(\varepsilon )}{i\omega _{n}-\varepsilon -\varepsilon '}}.}$

Appendix: Properties of distribution functions

Distribution functions

The general notation ${\displaystyle n_{\eta }}$ stands for either Bose (η = +1) or Fermi (η = −1) distribution function

${\displaystyle n_{\eta }(\xi )={\frac {1}{e^{\beta \xi }-\eta }}.}$

If necessary, the specific notations n_B and n_F are used to indicate Bose and Fermi distribution functions respectively

${\displaystyle n_{\eta }(\xi )={\begin{cases}n_{\rm {B}}(\xi ),&{\text{if }}\eta =+1,\\n_{\rm {F}}(\xi ),&{\text{if }}\eta =-1.\end{cases}}}$

Relation to hyperbolic functions

The Bose distribution function is related to hyperbolic cotangent function by

${\displaystyle n_{\rm {B}}(\xi )={\frac {1}{2}}\left(\operatorname {coth} {\frac {\beta \xi }{2}}-1\right).}$

The Fermi distribution function is related to hyperbolic tangent function by

${\displaystyle n_{\rm {F}}(\xi )={\frac {1}{2}}\left(1-\operatorname {tanh} {\frac {\beta \xi }{2}}\right).}$

Parity

Both distribution functions do not have definite parity,

${\displaystyle n_{\eta }(-\xi )=-\eta -n_{\eta }(\xi ).}$

Another formula is in terms of the ${\displaystyle c_{\eta }}$ function

${\displaystyle n_{\eta }(-\xi )=n_{\eta }(\xi )+2\xi c_{\eta }(0,\xi ).}$

However their derivatives have definite parity.

Bose–Fermi transmutation

Bose and Fermi distribution functions transmute under a shift of the variable by the fermionic frequency,

${\displaystyle n_{\eta }(i\omega _{m}+\xi )=-n_{-\eta }(\xi ).}$

However shifting by bosonic frequencies does not make any difference.

Derivatives

First order

${\displaystyle n_{\rm {B}}^{\prime }(\xi )=-{\frac {\beta }{4}}\mathrm {csch} ^{2}{\frac {\beta \xi }{2}},}$

${\displaystyle n_{\rm {F}}^{\prime }(\xi )=-{\frac {\beta }{4}}\mathrm {sech} ^{2}{\frac {\beta \xi }{2}}.}$

In terms of product:

${\displaystyle n_{\eta }^{\prime }(\xi )=-\beta n_{\eta }(\xi )(1+\eta n_{\eta }(\xi )).}$

In the zero temperature limit:

${\displaystyle n_{\eta }^{\prime }(\xi )=\eta \delta (\xi ){\text{ as }}\beta \rightarrow \infty .}$

Second order

${\displaystyle n_{\rm {B}}^{\prime \prime }(\xi )={\frac {\beta ^{2}}{4}}\operatorname {csch} ^{2}{\frac {\beta \xi }{2}}\operatorname {coth} {\frac {\beta \xi }{2}},}$

${\displaystyle n_{\rm {F}}^{\prime \prime }(\xi )={\frac {\beta ^{2}}{4}}\operatorname {sech} ^{2}{\frac {\beta \xi }{2}}\operatorname {tanh} {\frac {\beta \xi }{2}}.}$

Formula of difference

${\displaystyle n_{\eta }(a+b)-n_{\eta }(a-b)=-{\frac {\mathrm {sinh} \beta b}{\mathrm {cosh} \beta a-\eta \,\mathrm {cosh} \beta b}}.}$

Case a = 0

${\displaystyle n_{\rm {B}}(b)-n_{\rm {B}}(-b)=\mathrm {coth} {\frac {\beta b}{2}},}$

${\displaystyle n_{\rm {F}}(b)-n_{\rm {F}}(-b)=-\mathrm {tanh} {\frac {\beta b}{2}}.}$

Case a → 0

${\displaystyle n_{\rm {B}}(a+b)-n_{\rm {B}}(a-b)=\operatorname {coth} {\frac {\beta b}{2}}+n_{\rm {B}}^{\prime \prime }(b)a^{2}+\cdots ,}$

${\displaystyle n_{\rm {F}}(a+b)-n_{\rm {F}}(a-b)=-\operatorname {tanh} {\frac {\beta b}{2}}+n_{\rm {F}}^{\prime \prime }(b)a^{2}+\cdots .}$

Case b → 0

${\displaystyle n_{\rm {B}}(a+b)-n_{\rm {B}}(a-b)=2n_{\rm {B}}^{\prime }(a)b+\cdots ,}$

${\displaystyle n_{\rm {F}}(a+b)-n_{\rm {F}}(a-b)=2n_{\rm {F}}^{\prime }(a)b+\cdots .}$

The function c_η

Definition:

${\displaystyle c_{\eta }(a,b)\equiv -{\frac {n_{\eta }(a+b)-n_{\eta }(a-b)}{2b}}.}$

For Bose and Fermi type:

${\displaystyle c_{\rm {B}}(a,b)\equiv c_{+}(a,b),}$

${\displaystyle c_{\rm {F}}(a,b)\equiv c_{-}(a,b).}$

Relation to hyperbolic functions

${\displaystyle c_{\eta }(a,b)={\frac {\sinh \beta b}{2b(\cosh \beta a-\eta \cosh \beta b)}}.}$

It is obvious that ${\displaystyle c_{\rm {F}}(a,b)}$ is positive definite.

To avoid overflow in the numerical calculation, the tanh and coth functions are used

${\displaystyle c_{\rm {B}}(a,b)={\frac {1}{4b}}\left(\operatorname {coth} {\frac {\beta (a-b)}{2}}-\operatorname {coth} {\frac {\beta (a+b)}{2}}\right),}$

${\displaystyle c_{\rm {F}}(a,b)={\frac {1}{4b}}\left(\operatorname {tanh} {\frac {\beta (a+b)}{2}}-\operatorname {tanh} {\frac {\beta (a-b)}{2}}\right).}$

Case a = 0

${\displaystyle c_{\rm {B}}(0,b)=-{\frac {1}{2b}}\operatorname {coth} {\frac {\beta b}{2}},}$

${\displaystyle c_{\rm {F}}(0,b)={\frac {1}{2b}}\operatorname {tanh} {\frac {\beta b}{2}}.}$

Case b = 0

${\displaystyle c_{\rm {B}}(a,0)={\frac {\beta }{4}}\operatorname {csch} ^{2}{\frac {\beta a}{2}},}$

${\displaystyle c_{\rm {F}}(a,0)={\frac {\beta }{4}}\operatorname {sech} ^{2}{\frac {\beta a}{2}}.}$

Low temperature limit

For a = 0: ${\displaystyle c_{\rm {F}}(0,b)={\frac {1}{2|b|}}.}$

For b = 0: ${\displaystyle c_{\rm {F}}(a,0)=\delta (a).}$

In general,

${\displaystyle c_{\rm {F}}(a,b)={\begin{cases}{\frac {1}{2|b|}},&{\text{if }}|a|<|b|\\0,&{\text{if }}|a|>|b|\end{cases}}}$

See also

• Imaginary time
• Thermal quantum field theory

External links

Agustin Nieto: Evaluating Sums over the Matsubara Frequencies. arXiv:hep-ph/9311210

Github repository: MatsubaraSum A Mathematica package for Matsubara frequency summation.

A. Taheridehkordi, S. Curnoe, J.P.F. LeBlanc: Algorithmic Matsubara Integration for Hubbard-like models.. arXiv:cond-mat/1808.05188

References

1. Altland, Alexander; Simons, Ben D. (2010-03-11). Condensed Matter Field Theory. Cambridge University Press. doi:10.1017/cbo9780511789984. ISBN   978-0-521-76975-4.
2. A. Abrikosov, L. Gor'kov, I. Dzyaloshinskii: Methods of Quantum Field Theory in Statistical Physics., New York, Dover Publ., 1975, ISBN   0-486-63228-8
3. [Piers Coleman]: Introduction to Many-Body Physics., Cambridge University Press., 2015, ISBN   978-0-521-86488-6
4. Mahan, Gerald D. (2000). Many-particle physics (3rd ed.). New York: Kluwer Academic/Plenum Publishers. ISBN   0-306-46338-5. OCLC   43864386.
5. Summation of series: Sommerfeld-Watson transformation, Lecture notes , M. G. Rozman