
The accelerating expansion of the universe is the observation that the expansion of the universe is such that the velocity at which a distant galaxy is receding from the observer is continuously increasing with time.

Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that:
- Objects observed in deep space—extragalactic space, 10 megaparsecs (Mpc) or more—are found to have a redshift, interpreted as a relative velocity away from Earth;
- This Doppler shift-measured velocity of various galaxies receding from the Earth is approximately proportional to their distance from the Earth for galaxies up to a few hundred megaparsecs away.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
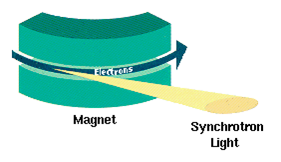
Synchrotron radiation is the electromagnetic radiation emitted when charged particles are accelerated radially, i.e., when they are subject to an acceleration perpendicular to their velocity. It is produced, for example, in synchrotrons using bending magnets, undulators and/or wigglers. If the particle is non-relativistic, then the emission is called cyclotron emission. If, on the other hand, the particles are relativistic, sometimes referred to as ultrarelativistic, the emission is called synchrotron emission. Synchrotron radiation may be achieved artificially in synchrotrons or storage rings, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over the entire electromagnetic spectrum which is also called continuum radiation.
Peculiar motion or peculiar velocity refers to the velocity of an object relative to a rest frame — usually a frame in which the average velocity of some objects is zero.
The particle horizon is the maximum distance from which light from particles could have traveled to the observer in the age of the universe. Much like the concept of a terrestrial horizon, it represents the boundary between the observable and the unobservable regions of the universe, so its distance at the present epoch defines the size of the observable universe. Due to the expansion of the universe it is not simply the age of the universe times the speed of light, but rather the speed of light times the conformal time. The existence, properties, and significance of a cosmological horizon depend on the particular cosmological model.

In relativity, proper time along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and a Lorentz scalar. The proper time interval between two events on a world line is the change in proper time. This interval is the quantity of interest, since proper time itself is fixed only up to an arbitrary additive constant, namely the setting of the clock at some event along the world line. The proper time interval between two events depends not only on the events but also the world line connecting them, and hence on the motion of the clock between the events. It is expressed as an integral over the world line. An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated (inertial) clock between the same two events. The twin paradox is an example of this effect.

The Kerr–Newman metric is a solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding a charged, rotating mass. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge. The solution has instead been of primarily theoretical and mathematical interest.
The angular diameter distance is a distance measure used in astronomy. It is defined in terms of an object's physical size, , and the angular size of the object as viewed from earth.
The angular diameter distance depends on the assumed cosmology of the universe. The angular diameter distance to an object at redshift, , is expressed in terms of the comoving distance, as:
Where is the FLRW coordinate defined as:
Where is the curvature density and is the value of the Hubble parameter today.
Luminosity distanceDL is defined in terms of the relationship between the absolute magnitude M and apparent magnitude m of an astronomical object.

In relativistic physics, the Born coordinate chart is a coordinate chart for Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds, so called Langevin observers. This chart is often attributed to Max Born, due to his 1909 work on the relativistic physics of a rotating body. For overview of the application of accelerations in flat spacetime, see Acceleration and proper reference frame.

The deceleration parameter in cosmology is a dimensionless measure of the cosmic acceleration of the expansion of space in a Friedmann–Lemaître–Robertson–Walker universe. It is defined by:

Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly observable, but is more convenient for calculations. The distance measures discussed here all reduce to the common notion of Euclidean distance at low redshift.

The Dark Energy Survey (DES) is a visible and near-infrared survey that aims to probe the dynamics of the expansion of the Universe and the growth of large-scale structure. The collaboration is composed of research institutions and universities from the United States, Brazil, the United Kingdom, Germany, Spain, and Switzerland.

In cosmology, baryon acoustic oscillations (BAO) are fluctuations in the density of the visible baryonic matter of the universe, caused by acoustic density waves in the primordial plasma of the early universe. In the same way that supernovae provide a "standard candle" for astronomical observations, BAO matter clustering provides a "standard ruler" for length scale in cosmology. The length of this standard ruler is given by the maximum distance the acoustic waves could travel in the primordial plasma before the plasma cooled to the point where it became neutral atoms, which stopped the expansion of the plasma density waves, "freezing" them into place. The length of this standard ruler can be measured by looking at the large scale structure of matter using astronomical surveys. BAO measurements help cosmologists understand more about the nature of dark energy by constraining cosmological parameters.
In 1989 Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy. Bowring rewrote the fourth order Redfearn series in a more compact notation by replacing the spherical terms, i.e. those independent of ellipticity, by the exact expressions used in the spherical transverse Mercator projection. There was no gain in accuracy since the elliptic terms were still truncated at the 1mm level. Such modifications were of possible use when computing resources were minimal.
Multipole radiation is a theoretical framework for the description of electromagnetic or gravitational radiation from time-dependent distributions of distant sources. These tools are applied to physical phenomena which occur at a variety of length scales - from gravitational waves due to galaxy collisions to gamma radiation resulting from nuclear decay. Multipole radiation is analyzed using similar multipole expansion techniques that describe fields from static sources, however there are important differences in the details of the analysis because multipole radiation fields behave quite differently from static fields. This article is primarily concerned with electromagnetic multipole radiation, although the treatment of gravitational waves is similar.





























