
In mathematics, many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group acts also on triangles by transforming triangles into triangles.

In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of n elements is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).
In mathematics, a building is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces. Buildings were initially introduced by Jacques Tits as a means to understand the structure of isotropic reductive linear algebraic groups over arbitrary fields. The more specialized theory of Bruhat–Tits buildings plays a role in the study of p-adic Lie groups analogous to that of the theory of symmetric spaces in the theory of Lie groups.

In the mathematical field of Lie theory, a Dynkin diagram, named for Eugene Dynkin, is a type of graph with some edges doubled or tripled. Dynkin diagrams arise in the classification of semisimple Lie algebras over algebraically closed fields, in the classification of Weyl groups and other finite reflection groups, and in other contexts. Various properties of the Dynkin diagram correspond to important features of the associated Lie algebra.

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.

In the area of modern algebra known as group theory, the Conway groups are the three sporadic simple groups Co1, Co2 and Co3 along with the related finite group Co0 introduced by (Conway 1968, 1969).

In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here, PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

In the area of modern algebra known as group theory, the Higman–Sims group HS is a sporadic simple group of order
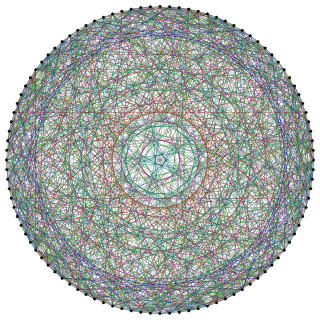
In mathematical graph theory, the Higman–Sims graph is a 22-regular undirected graph with 100 vertices and 1100 edges. It is the unique strongly regular graph srg(100,22,0,6), where no neighboring pair of vertices share a common neighbor and each non-neighboring pair of vertices share six common neighbors. It was first constructed by Mesner (1956) and rediscovered in 1968 by Donald G. Higman and Charles C. Sims as a way to define the Higman–Sims group, a subgroup of index two in the group of automorphisms of the Hoffman–Singleton graph.
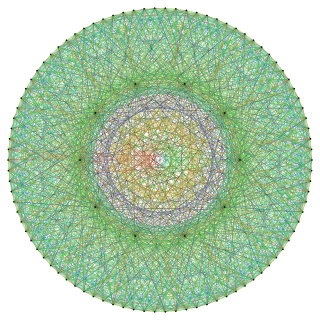
In the mathematical field of graph theory, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular undirected graph with 100 vertices and 1800 edges.

In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphism

In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y. Distance-transitive graphs were first defined in 1971 by Norman L. Biggs and D. H. Smith.

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

In the area of modern algebra known as group theory, the Janko groupJ1 is a sporadic simple group of order

In the area of modern algebra known as group theory, the Janko groupJ2 or the Hall-Janko groupHJ is a sporadic simple group of order

In the area of modern algebra known as group theory, the McLaughlin group McL is a sporadic simple group of order
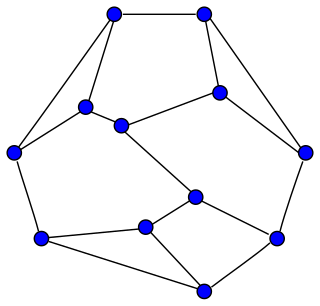
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.

The 110-vertex Iofinova–Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.











