Related Research Articles

In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

Flux describes any effect that appears to pass or travel through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface.
A dimensionless quantity is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one, which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time. Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians.
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.
Flow measurement is the quantification of bulk fluid movement. Flow can be measured in a variety of ways. The common types of flowmeters with industrial applications are listed below:
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.
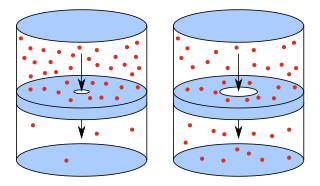
In physics and chemistry, effusion is the process in which a gas escapes from a container through a hole of diameter considerably smaller than the mean free path of the molecules. Such a hole is often described as a pinhole and the escape of the gas is due to the pressure difference between the container and the exterior. Under these conditions, essentially all molecules which arrive at the hole continue and pass through the hole, since collisions between molecules in the region of the hole are negligible. Conversely, when the diameter is larger than the mean free path of the gas, flow obeys the Sampson flow law.
Hemodynamics or haemodynamics are the dynamics of blood flow. The circulatory system is controlled by homeostatic mechanisms of autoregulation, just as hydraulic circuits are controlled by control systems. The hemodynamic response continuously monitors and adjusts to conditions in the body and its environment. Hemodynamics explains the physical laws that govern the flow of blood in the blood vessels.
Permeability in fluid mechanics and the Earth sciences is a measure of the ability of a porous material to allow fluids to pass through it.
The heat transfer coefficient or film coefficient, or film effectiveness, in thermodynamics and in mechanics is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat :
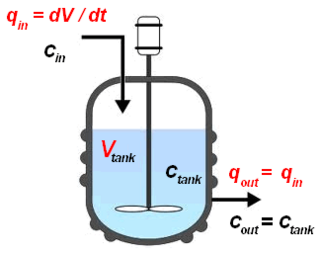
The continuous stirred-tank reactor (CSTR), also known as vat- or backmix reactor, mixed flow reactor (MFR), or a continuous-flow stirred-tank reactor (CFSTR), is a common model for a chemical reactor in chemical engineering and environmental engineering. A CSTR often refers to a model used to estimate the key unit operation variables when using a continuous agitated-tank reactor to reach a specified output. The mathematical model works for all fluids: liquids, gases, and slurries.
Fluid mechanics is the branch of physics concerned with the mechanics of fluids and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology.

The plug flow reactor model is a model used to describe chemical reactions in continuous, flowing systems of cylindrical geometry. The PFR model is used to predict the behavior of chemical reactors of such design, so that key reactor variables, such as the dimensions of the reactor, can be estimated.

In classical field theories, the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the pathline of the parcel. This can be visualized as sitting in a boat and drifting down a river.

The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Shear velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. It is useful as a method in fluid mechanics to compare true velocities, such as the velocity of a flow in a stream, to a velocity that relates shear between layers of flow.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

The Reynolds number helps predict flow patterns in different fluid flow situations. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. Reynolds numbers are an important dimensionless quantity in fluid mechanics.
Heat transfer enhancement is the process of increasing the effectiveness of heat exchangers. This can be achieved when the heat transfer power of a given device is increased or when the pressure losses generated by the device are reduced. A variety of techniques can be applied to this effect, including generating strong secondary flows or increasing boundary layer turbulence.
The residence time of a fluid parcel is the total time that the parcel has spent inside a control volume. The residence time of a set of parcels is quantified in terms of the frequency distribution of the residence time in the set, which is known as residence time distribution (RTD), or in terms of its average, known as mean residence time.
References
- Craik, Alex D. D. (1988), Wave interactions and fluid flows, Cambridge University Press, ISBN 978-0-521-36829-2
- Tennekes, Hendrik; Lumley, John L. (1972), A first course in turbulence, MIT Press, ISBN 978-0-262-20019-6