Brownian motion is the random motion of particles suspended in a medium.
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.
In statistical mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force, with that of the total potential energy of the system. Mathematically, the theorem states
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by , , or and is measured in W·m−1·K−1.
The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. It treats a gas as composed of numerous particles, too small to see with a microscope, which are constantly in random motion. Their collisions with each other and with the walls of their container are used to explain physical properties of the gas—for example, the relationship between its temperature, pressure, and volume. The particles are now known to be the atoms or molecules of the gas.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.
In physics, mean free path is the average distance over which a moving particle travels before substantially changing its direction or energy, typically as a result of one or more successive collisions with other particles.
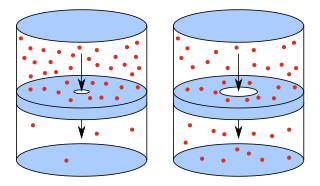
In physics and chemistry, effusion is the process in which a gas escapes from a container through a hole of diameter considerably smaller than the mean free path of the molecules. Such a hole is often described as a pinhole and the escape of the gas is due to the pressure difference between the container and the exterior. Under these conditions, essentially all molecules which arrive at the hole continue and pass through the hole, since collisions between molecules in the region of the hole are negligible. Conversely, when the diameter is larger than the mean free path of the gas, flow obeys the Sampson flow law.
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and λ (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant:
In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.
A Knudsen gas is a gas in a state of such low density that the average distance travelled by the gas molecules between collisions is greater than the diameter of the receptacle that contains it. If the mean free path is much greater than the diameter, the flow regime is dominated by collisions between the gas molecules and the walls of the receptacle, rather than intermolecular collisions with each other. It is named after Martin Knudsen.
Direct simulation Monte Carlo (DSMC) method uses probabilistic Monte Carlo simulation to solve the Boltzmann equation for finite Knudsen number fluid flows.
Rotational diffusion is the rotational movement which acts upon any object such as particles, molecules, atoms when present in a fluid, by random changes in their orientations. Whilst the directions and intensities of these changes are statistically random, they do not arise randomly and are instead the result of interactions between particles. One example occurs in colloids, where relatively large insoluble particles are suspended in a greater amount of fluid. The changes in orientation occur from collisions between the particle and the many molecules forming the fluid surrounding the particle, which each transfer kinetic energy to the particle, and as such can be considered random due to the varied speeds and amounts of fluid molecules incident on each individual particle at any given time.
In physics, statistics, econometrics and signal processing, a stochastic process is said to be in an ergodic regime if an observable's ensemble average equals the time average. In this regime, any collection of random samples from a process must represent the average statistical properties of the entire regime. Conversely, a regime of a process that is not ergodic is said to be in non-ergodic regime. A regime implies a time-window of a process whereby ergodicity measure is applied.
Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one.
Kinetic diameter is a measure applied to atoms and molecules that expresses the likelihood that a molecule in a gas will collide with another molecule. It is an indication of the size of the molecule as a target. The kinetic diameter is not the same as atomic diameter defined in terms of the size of the atom's electron shell, which is generally a lot smaller, depending on the exact definition used. Rather, it is the size of the sphere of influence that can lead to a scattering event.
In physics, chemistry and related fields, a kinetic scheme is a network of states and connections between them representing a dynamical process. Usually a kinetic scheme represents a Markovian process, while for non-Markovian processes generalized kinetic schemes are used. Figure 1 illustrates a kinetic scheme.
The residence time of a fluid parcel is the total time that the parcel has spent inside a control volume (e.g.: a chemical reactor, a lake, a human body). The residence time of a set of parcels is quantified in terms of the frequency distribution of the residence time in the set, which is known as residence time distribution (RTD), or in terms of its average, known as mean residence time.
