
In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.
Distributions are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions than classical solutions, or appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta function.
In mathematics, particularly linear algebra and functional analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized. This is extremely useful because computations involving a diagonalizable matrix can often be reduced to much simpler computations involving the corresponding diagonal matrix. The concept of diagonalization is relatively straightforward for operators on finite-dimensional vector spaces but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modeled by multiplication operators, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory for a historical perspective.

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common method used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold, that measures the extent to which the metric tensor is not locally isometric to that of Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional plane σp in the tangent space at a point p of the manifold. It is the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a smooth real-valued function on the 2-Grassmannian bundle over the manifold.

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analog of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In functional analysis and related branches of mathematics, the Banach–Alaoglu theorem states that the closed unit ball of the dual space of a normed vector space is compact in the weak* topology. A common proof identifies the unit ball with the weak* topology as a closed subset of a product of compact sets with the product topology. As a consequence of Tychonoff's theorem, this product, and hence the unit ball within, is compact.
In linear algebra, the Gram matrix of a set of vectors in an inner product space is the Hermitian matrix of inner products, whose entries are given by .
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic. The Weyl tensor differs from the Riemann curvature tensor in that it does not convey information on how the volume of the body changes, but rather only how the shape of the body is distorted by the tidal force. The Ricci curvature, or trace component of the Riemann tensor contains precisely the information about how volumes change in the presence of tidal forces, so the Weyl tensor is the traceless component of the Riemann tensor. It is a tensor that has the same symmetries as the Riemann tensor with the extra condition that it be trace-free: metric contraction on any pair of indices yields zero.
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami operator, after Laplace and Eugenio Beltrami. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence of the gradient, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterior derivative. The resulting operator is called the Laplace–de Rham operator.
In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, on a complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study.
In quantum field theory and statistical mechanics, the Mermin–Wagner theorem states that continuous symmetries cannot be spontaneously broken at finite temperature in systems with sufficiently short-range interactions in dimensions d ≤ 2. Intuitively, this means that long-range fluctuations can be created with little energy cost and since they increase the entropy they are favored.

In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint.
In mathematics, a metric connection is a connection in a vector bundle E equipped with a bundle metric; that is, a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve. Other common equivalent formulations of a metric connection include:
In mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity, named after Roland Weitzenböck, expresses a relationship between two second-order elliptic operators on a manifold with the same leading symbol. Usually Weitzenböck formulae are implemented for G-invariant self-adjoint operators between vector bundles associated to some principal G-bundle, although the precise conditions under which such a formula exists are difficult to formulate. This article focuses on three examples of Weitzenböck identities: from Riemannian geometry, spin geometry, and complex analysis.

In mathematics, a genus of a multiplicative sequence is a ring homomorphism, from the ring of smooth compact manifolds up to the equivalence of bounding a smooth manifold with boundary to another ring, usually the rational numbers, having the property that they are constructed from a sequence of polynomials in characteristic classes that arise as coefficients in formal power series with good multiplicative properties.
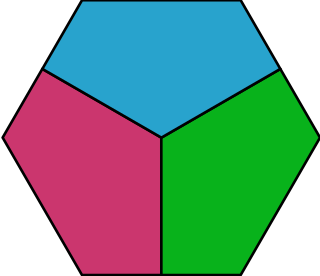
The Borsuk problem in geometry, for historical reasons incorrectly called Borsuk's conjecture, is a question in discrete geometry.
The cluster-expansion approach is a technique in quantum mechanics that systematically truncates the BBGKY hierarchy problem that arises when quantum dynamics of interacting systems is solved. This method is well suited for producing a closed set of numerically computable equations that can be applied to analyze a great variety of many-body and/or quantum-optical problems. For example, it is widely applied in semiconductor quantum optics and it can be applied to generalize the semiconductor Bloch equations and semiconductor luminescence equations.

























