
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime.

In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
Invariance of domain is a theorem in topology about homeomorphic subsets of Euclidean space . It states:

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

Commutative algebra, first known as ideal theory, is the branch of algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra. Prominent examples of commutative rings include polynomial rings; rings of algebraic integers, including the ordinary integers ; and p-adic integers.

In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.

Jean Dominique Antony Metzinger was a major 20th-century French painter, theorist, writer, critic and poet, who along with Albert Gleizes wrote the first theoretical work on Cubism. His earliest works, from 1900 to 1904, were influenced by the neo-Impressionism of Georges Seurat and Henri-Edmond Cross. Between 1904 and 1907 Metzinger worked in the Divisionist and Fauvist styles with a strong Cézannian component, leading to some of the first proto-Cubist works.

Pierre René, Viscount Deligne is a Belgian mathematician. He is best known for work on the Weil conjectures, leading to a complete proof in 1973. He is the winner of the 2013 Abel Prize, 2008 Wolf Prize, 1988 Crafoord Prize, and 1978 Fields Medal.

Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the Commanding General of the École Polytechnique. He is considered a reviver of projective geometry, and his work Traité des propriétés projectives des figures is considered the first definitive text on the subject since Gérard Desargues' work on it in the 17th century. He later wrote an introduction to it: Applications d'analyse et de géométrie.

In mathematics, arithmetic geometry is roughly the application of techniques from algebraic geometry to problems in number theory. Arithmetic geometry is centered around Diophantine geometry, the study of rational points of algebraic varieties.

Jean Paul de Gua de Malves was a French mathematician who published in 1740 a work on analytical geometry in which he applied it, without the aid of differential calculus, to find the tangents, asymptotes, and various singular points of an algebraic curve.

Jean Baptiste Marie Charles Meusnier de la Place was a French mathematician, engineer and Revolutionary general. He is best known for Meusnier's theorem on the curvature of surfaces, which he formulated while he was at the École Royale du Génie. He also discovered the helicoid. He worked with Lavoisier on the decomposition of water and the evolution of hydrogen.

Jean-Michel Bismut is a French mathematician who has been a professor at the Université Paris-Sud since 1981. His mathematical career covers two apparently different branches of mathematics: probability theory and differential geometry. Ideas from probability play an important role in his works on geometry.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

George David Birkhoff was an American mathematician best known for what is now called the ergodic theorem. Birkhoff was one of the most important leaders in American mathematics in his generation, and during his time he was considered by many to be the preeminent American mathematician.

La Femme au Cheval is a large oil painting created toward the end of 1911, early 1912, by the French artist Jean Metzinger (1883–1956). The work was exhibited in Paris at the Salon des Indépendants in 1912 and the Salon de la Section d'Or, 1912. The following year La Femme au Cheval was reproduced in The Cubist Painters, Aesthetic Meditations by Guillaume Apollinaire (1913).
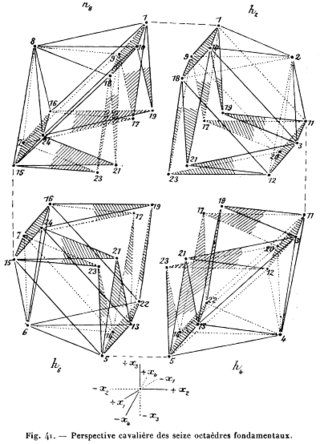
New possibilities opened up by the concept of four-dimensional space helped inspire many modern artists in the first half of the twentieth century. Early Cubists, Surrealists, Futurists, and abstract artists took ideas from higher-dimensional mathematics and used them to radically advance their work.
















