In algebraic number theory, Minkowski's bound gives an upper bound of the norm of ideals to be checked in order to determine the class number of a number field K. It is named for the mathematician Hermann Minkowski.
Let D be the discriminant of the field, n be the degree of K over , and be the number of complex embeddings where is the number of real embeddings. Then every class in the ideal class group of K contains an integral ideal of norm not exceeding Minkowski's bound
Minkowski's constant for the field K is this bound MK. [1]
Since the number of integral ideals of given norm is finite, the finiteness of the class number is an immediate consequence, [1] and further, the ideal class group is generated by the prime ideals of norm at most MK.
Minkowski's bound may be used to derive a lower bound for the discriminant of a field K given n, r1 and r2. Since an integral ideal has norm at least one, we have 1 ≤ MK, so that
For n at least 2, it is easy to show that the lower bound is greater than 1, so we obtain Minkowski's Theorem, that the discriminant of every number field, other than Q, is non-trivial. This implies that the field of rational numbers has no unramified extension.
The result is a consequence of Minkowski's theorem.
In mathematics, more specifically in ring theory, a Euclidean domain is an integral domain that can be endowed with a Euclidean function which allows a suitable generalization of the Euclidean division of integers. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them. Also every ideal in a Euclidean domain is principal, which implies a suitable generalization of the fundamental theorem of arithmetic: every Euclidean domain is a unique factorization domain.
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.
In mathematics, a unique factorization domain (UFD) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of irreducible elements, uniquely up to order and units.
In number theory, the ideal class group of an algebraic number field K is the quotient group JK /PK where JK is the group of fractional ideals of the ring of integers of K, and PK is its subgroup of principal ideals. The class group is a measure of the extent to which unique factorization fails in the ring of integers of K. The order of the group, which is finite, is called the class number of K.
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).
In mathematics, Felix Klein's j-invariant or j function, regarded as a function of a complex variable τ, is a modular function of weight zero for SL(2, Z) defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that
In algebraic number theory, a quadratic field is an algebraic number field of degree two over , the rational numbers.
In commutative algebra, the norm of an ideal is a generalization of a norm of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal of a complicated number ring in terms of an ideal in a less complicated ring. When the less complicated number ring is taken to be the ring of integers, Z, then the norm of a nonzero ideal I of a number ring R is simply the size of the finite quotient ring R/I.
In mathematics, an order in the sense of ring theory is a subring of a ring , such that
Abstract analytic number theory is a branch of mathematics which takes the ideas and techniques of classical analytic number theory and applies them to a variety of different mathematical fields. The classical prime number theorem serves as a prototypical example, and the emphasis is on abstract asymptotic distribution results. The theory was invented and developed by mathematicians such as John Knopfmacher and Arne Beurling in the twentieth century.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
In algebraic number theory, the different ideal is defined to measure the (possible) lack of duality in the ring of integers of an algebraic number field K, with respect to the field trace. It then encodes the ramification data for prime ideals of the ring of integers. It was introduced by Richard Dedekind in 1882.
In mathematics, a Kloosterman sum is a particular kind of exponential sum. They are named for the Dutch mathematician Hendrik Kloosterman, who introduced them in 1926 when he adapted the Hardy–Littlewood circle method to tackle a problem involving positive definite diagonal quadratic forms in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924.
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function.
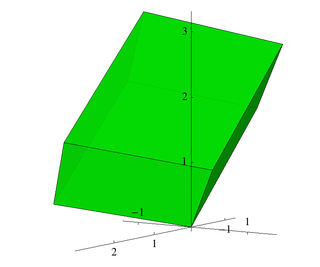
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field. More specifically, it is proportional to the squared volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified.
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function f of a complex argument z and an operator T, the aim is to construct an operator, f(T), which naturally extends the function f from complex argument to operator argument. More precisely, the functional calculus defines a continuous algebra homomorphism from the holomorphic functions on a neighbourhood of the spectrum of T to the bounded operators.
In algebraic number theory, a fundamental unit is a generator for the unit group of the ring of integers of a number field, when that group has rank 1. Dirichlet's unit theorem shows that the unit group has rank 1 exactly when the number field is a real quadratic field, a complex cubic field, or a totally imaginary quartic field. When the unit group has rank ≥ 1, a basis of it modulo its torsion is called a fundamental system of units. Some authors use the term fundamental unit to mean any element of a fundamental system of units, not restricting to the case of rank 1.
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann, after whom it is named.
In mathematics, an algebraic number field is an extension field of the field of rational numbers such that the field extension has finite degree . Thus is a field that contains and has finite dimension when considered as a vector space over .
In mathematics, especially in algebraic number theory, the Hermite–Minkowski theorem states that for any integer N there are only finitely many number fields, i.e., finite field extensions K of the rational numbers Q, such that the discriminant of K/Q is at most N. The theorem is named after Charles Hermite and Hermann Minkowski.
