Related Research Articles
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.

In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.
Statistical mechanics, one of the pillars of modern physics, describes how macroscopic observations are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various materials.
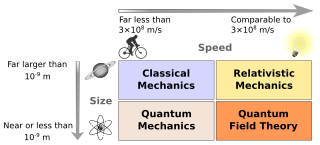
Classical physics is a group of physics theories that predate modern, more complete, or more widely applicable theories. If a currently accepted theory is considered to be modern, and its introduction represented a major paradigm shift, then the previous theories, or new theories based on the older paradigm, will often be referred to as belonging to the realm of "classical physics".
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, aircraft and ships. Structural analysis employs the fields of applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures.
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.

A porous medium or a porous material is a material containing pores (voids). The skeletal portion of the material is often called the "matrix" or "frame". The pores are typically filled with a fluid. The skeletal material is usually a solid, but structures like foams are often also usefully analyzed using concept of porous media.
In theoretical physics and applied mathematics, a field equation is a partial differential equation which determines the dynamics of a physical field, specifically the time evolution and spatial distribution of the field. The solutions to the equation are mathematical functions which correspond directly to the field, as functions of time and space. Since the field equation is a partial differential equation, there are families of solutions which represent a variety of physical possibilities. Usually, there is not just a single equation, but a set of coupled equations which must be solved simultaneously. Field equations are not ordinary differential equations since a field depends on space and time, which requires at least two variables.
Fluid mechanics is the branch of physics concerned with the mechanics of fluids and the forces on them. It has applications in a wide range of disciplines, including mechanical, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology.
Poromechanics is a branch of physics and specifically continuum mechanics and acoustics that studies the behaviour of fluid-saturated porous media. A porous medium or a porous material is a solid permeated by an interconnected network of pores (voids) filled with a fluid. Usually both solid matrix and the pore network are assumed to be continuous, so as to form two interpenetrating continua such as in a sponge. Many natural substances such as rocks, soils, biological tissues, and man made materials such as foams and ceramics can be considered as porous media. Porous media whose solid matrix is elastic and the fluid is viscous are called poroelastic. A poroelastic medium is characterised by its porosity, permeability as well as the properties of its constituents.
FEFLOW is a computer program for simulating groundwater flow, mass transfer and heat transfer in porous media and fractured media. The program uses finite element analysis to solve the groundwater flow equation of both saturated and unsaturated conditions as well as mass and heat transport, including fluid density effects and chemical kinetics for multi-component reaction systems.
Continuum theories or models explain variation as involving gradual quantitative transitions without abrupt changes or discontinuities. In contrast, categorical theories or models explain variation using qualitatively different states.

Physics deals with the combination of matter and energy. It also deals with a wide variety of systems, about which theories have been developed that are used by physicists. In general, theories are experimentally tested numerous times before they are accepted as correct as a description of Nature. For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These "central theories" are important tools for research in more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.

Keith E. Gubbins is a British born American chemical engineer who is the W.H. Clark Distinguished University Professor of Chemical Engineering at North Carolina State University in Raleigh, NC. He is a member of the National Academy of Engineering in the chemistry section.

Krzysztof Wilmanski was a Polish-German scientist working in the fields of continuum mechanics and thermodynamics.
Ahmet Cemal Eringen was a Turkish- American engineering scientist. He was a professor at Princeton University and the founder of the Society of Engineering Science. The Eringen Medal is named in his honor.
In computational chemistry, a solvent model is a computational method that accounts for the behavior of solvated condensed phases. Solvent models enable simulations and thermodynamic calculations applicable to reactions and processes which take place in solution. These include biological, chemical and environmental processes. Such calculations can lead to new predictions about the physical processes occurring by improved understanding.
The governing equations of a mathematical model describe how the values of the unknown variables change when one or more of the known variables change.
Computational materials science and engineering uses modeling, simulation, theory, and informatics to understand materials. Main goals include discovering new materials, determining material behavior and mechanisms, explaining experiments, and exploring materials theories. It is analogous to computational chemistry and computational biology as an increasingly important subfield of materials science.
References
- ↑ Bowen,R. M. (1976). Eringen, A. C. (ed.). Theory of Mixtures, Part I. Continuum Physics. III. New York, USA: Academic Press.
- ↑ Wilmanski, Krzysztof (1996). "Porous Media at Finite Strains. The New Model with the Balance Equation of Porosity". Archives of Mechanics. 48 (4): 591–628.
- ↑ Wilmanski, Krzysztof (1998). Thermomechanics of Continua. Heidelberg, Germany: Springer.