In graph theory, the modular product of graphs G and H is a graph formed by combining G and H that has applications to subgraph isomorphism. It is one of several different kinds of graph products that have been studied, generally using the same vertex set (the Cartesian product of the sets of vertices of the two graphs G and H) but with different rules for determining which edges to include.
The vertex set of the modular product of G and H is the cartesian product V(G) × V(H). Any two vertices (u, v) and (u' , v' ) are adjacent in the modular product of G and H if and only if u is distinct from u', v is distinct from v', and either
Cliques in the modular product graph correspond to isomorphisms of induced subgraphs of G and H. Therefore, the modular product graph can be used to reduce problems of induced subgraph isomorphism to problems of finding cliques in graphs. Specifically, the maximum common induced subgraph of both G and H corresponds to the maximum clique in their modular product. Although the problems of finding largest common induced subgraphs and of finding maximum cliques are both NP-complete, this reduction allows clique-finding algorithms to be applied to the common subgraph problem.
In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.
In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set of vertices such that for every two vertices in , there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.
In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.
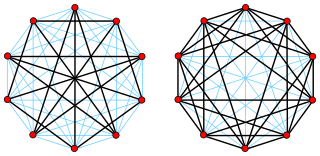
In the mathematical field of graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two distinct vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges connecting pairs of vertices in that subset.
In graph theory, a dominating set for a graph G is a subset D of its vertices, such that any vertex of G is either in D, or has a neighbor in D. The domination numberγ(G) is the number of vertices in a smallest dominating set for G.
In graph theory, a maximal independent set (MIS) or maximal stable set is an independent set that is not a subset of any other independent set. In other words, there is no vertex outside the independent set that may join it because it is maximal with respect to the independent set property.
In graph theory and theoretical computer science, a maximum common induced subgraph of two graphs G and H is a graph that is an induced subgraph of both G and H, and that has as many vertices as possible.
In complexity theory and graph theory, induced subgraph isomorphism is an NP-complete decision problem that involves finding a given graph as an induced subgraph of a larger graph.
In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge connects two squares on the same row (rank) or on the same column (file) as each other, the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape, and can be defined mathematically as the Cartesian product of two complete graphs, as the two-dimensional Hamming graphs, or as the line graphs of complete bipartite graphs.
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.
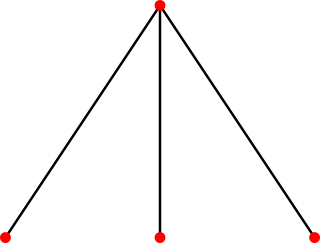
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.
In graph theory, a clique cover or partition into cliques of a given undirected graph is a partition of the vertices into cliques, subsets of vertices within which every two vertices are adjacent. A minimum clique cover is a clique cover that uses as few cliques as possible. The minimum k for which a clique cover exists is called the clique cover number of the given graph.
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
In graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.