Induced subgraph

Last updated October 21, 2024

In graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges, from the original graph, connecting pairs of vertices in that subset.

Definition

Formally, let $G=(V,E)$ be any graph, and let $S\subseteq V$ be any subset of vertices of $G$ . Then the induced subgraph $G[S]$ is the graph whose vertex set is $S$ and whose edge set consists of all of the edges in $E$ that have both endpoints in $S$ .^[1] That is, for any two vertices $u,v\in S$ , $u$ and $v$ are adjacent in $G[S]$ if and only if they are adjacent in $G$ . The same definition works for undirected graphs, directed graphs, and even multigraphs.

The induced subgraph $G[S]$ may also be called the subgraph induced in $G$ by $S$ , or (if context makes the choice of $G$ unambiguous) the induced subgraph of $S$ .

Examples

Important types of induced subgraphs include the following.

Induced paths are induced subgraphs that are paths. The shortest path between any two vertices in an unweighted graph is always an induced path, because any additional edges between pairs of vertices that could cause it to be not induced would also cause it to be not shortest. Conversely, in distance-hereditary graphs, every induced path is a shortest path.^[2]
Induced cycles are induced subgraphs that are cycles. The girth of a graph is defined by the length of its shortest cycle, which is always an induced cycle. According to the strong perfect graph theorem, induced cycles and their complements play a critical role in the characterization of perfect graphs.^[3]
Cliques and independent sets are induced subgraphs that are respectively complete graphs or edgeless graphs.
Induced matchings are induced subgraphs that are matchings.
The neighborhood of a vertex is the induced subgraph of all vertices adjacent to it.

Computation

The induced subgraph isomorphism problem is a form of the subgraph isomorphism problem in which the goal is to test whether one graph can be found as an induced subgraph of another. Because it includes the clique problem as a special case, it is NP-complete.^[4]

Related Research Articles

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets $and, that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.$

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph $is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.$

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In the mathematical discipline of graph theory, the line graph of an undirected graph $G$ is another graph $L(G)$ that represents the adjacencies between edges of $G$ . $L(G)$ is constructed in the following way: for each edge in $G$ , make a vertex in $L(G)$ ; for every two edges in $G$ that have a vertex in common, make an edge between their corresponding vertices in $L(G)$ .

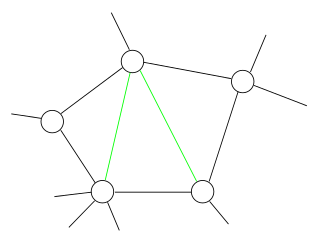
<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.

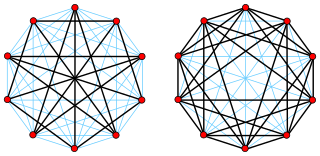
In the mathematical field of graph theory, the complement or inverse of a graph $G$ is a graph $H$ on the same vertices such that two distinct vertices of $H$ are adjacent if and only if they are not adjacent in $G$ . That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

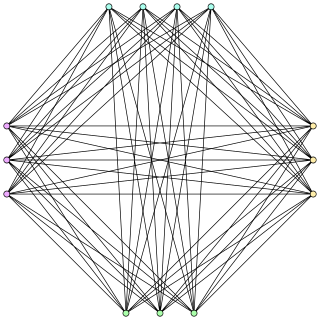
In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

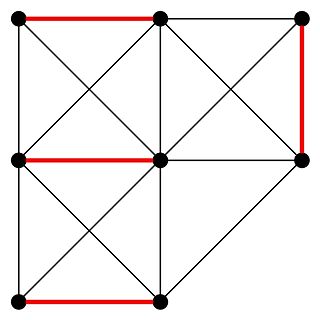
In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of finite undirected graphs with perfect matchings. It is a special case of the Tutte–Berge formula.

<span class="mw-page-title-main">Kőnig's theorem (graph theory)</span> Theorem showing that maximum matching and minimum vertex cover are equivalent for bipartite graphs

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

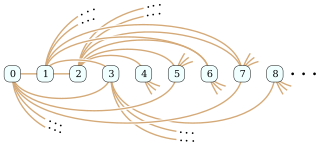
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

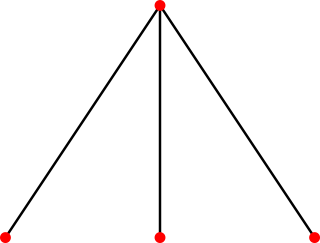
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

In graph theory, a clique cover or partition into cliques of a given undirected graph is a collection of cliques that cover the whole graph. A minimum clique cover is a clique cover that uses as few cliques as possible. The minimum $k$ for which a clique cover exists is called the clique cover number of the given graph.

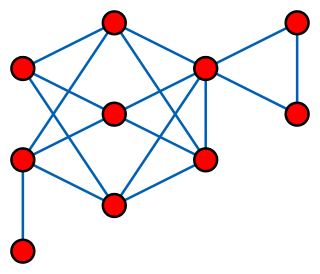
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of ⁠ $⁠$ vertices from an $n$ -vertex graph can partition the graph into disjoint subgraphs each of which has at most ⁠ $⁠$ vertices.

In the mathematical area of graph theory, an undirected graph $G$ is strongly chordal if it is a chordal graph and every cycle of even length in $G$ has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.

In graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.

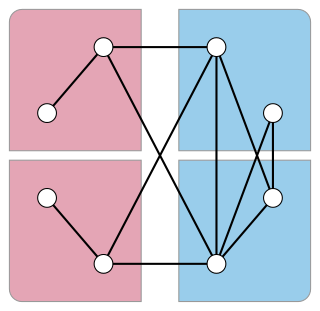
In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

In graph theory, a Ptolemaic graph is an undirected graph whose shortest path distances obey Ptolemy's inequality, which in turn was named after the Greek astronomer and mathematician Ptolemy. The Ptolemaic graphs are exactly the graphs that are both chordal and distance-hereditary; they include the block graphs and are a subclass of the perfect graphs.

References

↑ Diestel, Reinhard (2006), Graph Theory, Graduate texts in mathematics, vol. 173, Springer-Verlag, pp. 3–4, ISBN 9783540261834 .
↑ Howorka, Edward (1977), "A characterization of distance-hereditary graphs", The Quarterly Journal of Mathematics, Second Series, 28 (112): 417–420, doi:10.1093/qmath/28.4.417, MR 0485544 .
↑ Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem", Annals of Mathematics , 164 (1): 51–229, arXiv: math/0212070 , doi:10.4007/annals.2006.164.51, MR 2233847 .
↑ Johnson, David S. (1985), "The NP-completeness column: an ongoing guide", Journal of Algorithms, 6 (3): 434–451, doi:10.1016/0196-6774(85)90012-4, MR 0800733 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Diestel, Reinhard (2006), Graph Theory, Graduate texts in mathematics, vol. 173, Springer-Verlag, pp. 3–4, ISBN 9783540261834 .

[2] Howorka, Edward (1977), "A characterization of distance-hereditary graphs", The Quarterly Journal of Mathematics, Second Series, 28 (112): 417–420, doi:10.1093/qmath/28.4.417, MR 0485544 .

[3] Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem", Annals of Mathematics , 164 (1): 51–229, arXiv: math/0212070 , doi:10.4007/annals.2006.164.51, MR 2233847 .

[4] Johnson, David S. (1985), "The NP-completeness column: an ongoing guide", Journal of Algorithms, 6 (3): 434–451, doi:10.1016/0196-6774(85)90012-4, MR 0800733 .

[1]

[2]

[3]

[4]