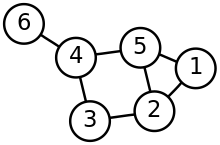
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
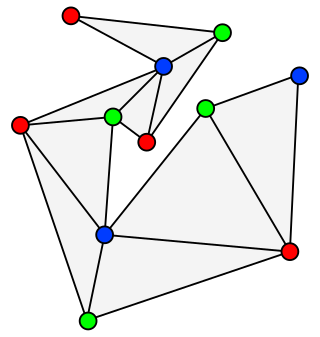
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

The Turán graph, denoted by , is a complete multipartite graph; it is formed by partitioning a set of vertices into subsets, with sizes as equal as possible, and then connecting two vertices by an edge if and only if they belong to different subsets. Where and are the quotient and remainder of dividing by , the graph is of the form , and the number of edges is
In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph.

Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. Results in extremal graph theory deal with quantitative connections between various graph properties, both global and local, and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In graph theory, a critical graph is an undirected graph all of whose subgraphs have smaller chromatic number. In such a graph, every vertex or edge is a critical element, in the sense that its deletion would decrease the number of colors needed in a graph coloring of the given graph. The decrease in the number of colors cannot be by more than one.

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
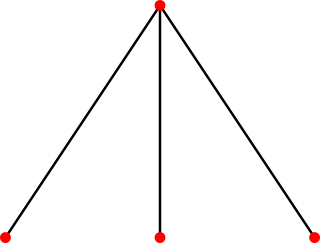
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.
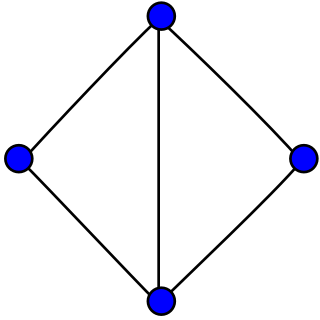
In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges. It consists of a complete graph minus one edge.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the same colour to a certain extent.

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
In graph theory, the act of coloring generally implies the assignment of labels to vertices, edges or faces in a graph. The incidence coloring is a special graph labeling where each incidence of an edge with a vertex is assigned a color under certain constraints.

In graph theory, a universal vertex is a vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph.

In combinatorial mathematics and extremal graph theory, the Ruzsa–Szemerédi problem or (6,3)-problem asks for the maximum number of edges in a graph in which every edge belongs to a unique triangle. Equivalently it asks for the maximum number of edges in a balanced bipartite graph whose edges can be partitioned into a linear number of induced matchings, or the maximum number of triples one can choose from points so that every six points contain at most two triples. The problem is named after Imre Z. Ruzsa and Endre Szemerédi, who first proved that its answer is smaller than by a slowly-growing factor.