Link (simplicial complex)

Last updated September 02, 2023

The tetrahedron is a 2-complex. Tetrahedron.svg — The tetrahedron is a 2-complex.

The link in a simplicial complex is a generalization of the neighborhood of a vertex in a graph. The link of a vertex encodes information about the local structure of the complex at the vertex.

Link of a vertex

Given an abstract simplicial complex $X$ and ${\textstyle v}$ a vertex in ${\textstyle V(X)}$ , its link ${\textstyle \operatorname {Lk} (v,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle v\not \in \tau }$ and ${\textstyle \tau \cup \{v\}}$ is a face of $X$ .

In the special case in which $X$ is a 1-dimensional complex (that is: a graph), ${\textstyle \operatorname {Lk} (v,X)}$ contains all vertices ${\textstyle u\neq v}$ such that ${\textstyle \{u,v\}}$ is an edge in the graph; that is, ${\textstyle \operatorname {Lk} (v,X)={\mathcal {N}}(v)=}$ the neighborhood of ${\textstyle v}$ in the graph.

Given a geometric simplicial complex $X$ and ${\textstyle v\in V(X)}$ , its link ${\textstyle \operatorname {Lk} (v,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle v\not \in \tau }$ and there is a simplex in ${\textstyle X}$ that has ${\textstyle v}$ as a vertex and ${\textstyle \tau }$ as a face.^[1]^: 3 Equivalently, the join ${\textstyle v\star \tau }$ is a face in ${\textstyle X}$ .^[2]^: 20

As an example, suppose v is the top vertex of the tetrahedron at the left. Then the link of v is the triangle at the base of the tetrahedron. This is because, for each edge of that triangle, the join of v with the edge is a triangle (one of the three triangles at the sides of the tetrahedron); and the join of v with the triangle itself is the entire tetrahedron.

The link of a vertex of a tetrahedron is the triangle.

An alternative definition is: the link of a vertex ${\textstyle v\in V(X)}$ is the graph $Lk(v, X)$ constructed as follows. The vertices of $Lk(v, X)$ are the edges of $X$ incident to $v$ . Two such edges are adjacent in $Lk(v, X)$ iff they are incident to a common 2-cell at $v$ .

The graph $Lk(v, X)$ is often given the topology of a ball of small radius centred at $v$ ; it is an analog to a sphere centered at a point.^[3]

Link of a face

The definition of a link can be extended from a single vertex to any face.

Given an abstract simplicial complex $X$ and any face ${\textstyle \sigma }$ of $X$ , its link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \sigma ,\tau }$ are disjoint and ${\textstyle \tau \cup \sigma }$ is a face of $X$ : ${\textstyle \operatorname {Lk} (\sigma ,X):=\{\tau \in X:~\tau \cap \sigma =\emptyset ,~\tau \cup \sigma \in X\}}$ .

Given a geometric simplicial complex $X$ and any face ${\textstyle \sigma \in X}$ , its link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \sigma ,\tau }$ are disjoint and there is a simplex in ${\textstyle X}$ that has both ${\textstyle \sigma }$ and ${\textstyle \tau }$ as faces.^[1]^: 3

Examples

The link of a vertex of a tetrahedron is a triangle – the three vertices of the link corresponds to the three edges incident to the vertex, and the three edges of the link correspond to the faces incident to the vertex. In this example, the link can be visualized by cutting off the vertex with a plane; formally, intersecting the tetrahedron with a plane near the vertex – the resulting cross-section is the link.

Another example is illustrated below. There is a two-dimensional simplicial complex. At the left, a vertex is marked in yellow. At the right, the link of that vertex is marked in green.

A vertex and its link.

Properties

For any simplicial complex $X$ , every link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is downward-closed, and therefore it is a simplicial complex too; it is a sub-complex of $X$ .
Because $X$ is simplicial, there is a set isomorphism between ${\textstyle \operatorname {Lk} (\sigma ,X)}$ and the set $X_{\sigma }:=\{\rho \in X{\text{ such that }}\sigma \subseteq \rho \}$ : every ${\textstyle \tau \in \operatorname {Lk} (\sigma ,X)}$ corresponds to ${\textstyle \tau \cup \sigma }$ , which is in $X_{\sigma }$ .

Link and star

A concept closely related to the link is the star.

Given an abstract simplicial complex $X$ and any face ${\textstyle \sigma \in X}$ , ${\textstyle V(X)}$ , its star ${\textstyle \operatorname {St} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \tau \cup \sigma }$ is a face of $X$ . In the special case in which $X$ is a 1-dimensional complex (that is: a graph), ${\textstyle \operatorname {St} (v,X)}$ contains all edges ${\textstyle \{u,v\}}$ for all vertices ${\textstyle u}$ that are neighbors of ${\textstyle v}$ . That is, it is a graph-theoretic star centered at ${\textstyle u}$ .

Given a geometric simplicial complex $X$ and any face ${\textstyle \sigma \in X}$ , its star ${\textstyle \operatorname {St} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that there is a simplex in ${\textstyle X}$ having both ${\textstyle \sigma }$ and ${\textstyle \tau }$ as faces: ${\textstyle \operatorname {St} (\sigma ,X):=\{\tau \in X:\exists \rho \in X:\tau ,\sigma {\text{ are faces of }}\rho \}}$ . In other words, it is the closure of the set ${\textstyle \{\rho \in X:\sigma {\text{ is a face of }}\rho \}}$ -- the set of simplices having ${\textstyle \sigma }$ as a face.

So the link is a subset of the star. The star and link are related as follows:

For any ${\textstyle \sigma \in X}$ , ${\textstyle \operatorname {Lk} (\sigma ,X)=\{\tau \in \operatorname {St} (\sigma ,X):\tau \cap \sigma =\emptyset \}}$ . ^[1]^: 3
For any ${\textstyle v\in V(X)}$ , ${\textstyle \operatorname {St} (v,X)=v\star \operatorname {Lk} (v,X)}$ , that is, the star of ${\textstyle v}$ is the cone of its link at ${\textstyle v}$ .^[2]^: 20

An example is illustrated below. There is a two-dimensional simplicial complex. At the left, a vertex is marked in yellow. At the right, the star of that vertex is marked in green.

A vertex and its star.

Related Research Articles

In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field K. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

<span class="mw-page-title-main">Simplex</span> Multi-dimensional generalization of triangle

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,

In statistics, Spearman's rank correlation coefficient or Spearman's ρ, named after Charles Spearman and often denoted by the Greek letter (rho) or as $, is a nonparametric measure of rank correlation. It assesses how well the relationship between two variables can be described using a monotonic function.$

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial complex from an abstract simplicial complex, the former is often called a geometric simplicial complex.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space.

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing families of expander graphs.

In probability theory, the Vysochanskij–Petunin inequality gives a lower bound for the probability that a random variable with finite variance lies within a certain number of standard deviations of the variable's mean, or equivalently an upper bound for the probability that it lies further away. The sole restrictions on the distribution are that it be unimodal and have finite variance.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

In algebraic topology, simplicial homology is the sequence of homology groups of a simplicial complex. It formalizes the idea of the number of holes of a given dimension in the complex. This generalizes the number of connected components.

In probability theory and statistics, given a stochastic process, the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. Autocovariance is closely related to the autocorrelation of the process in question.

In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).

In mathematics, the poset topology associated to a poset (S, ≤) is the Alexandrov topology (open sets are upper sets) on the poset of finite chains of (S, ≤), ordered by inclusion.

The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.

Discrete Morse theory is a combinatorial adaptation of Morse theory developed by Robin Forman. The theory has various practical applications in diverse fields of applied mathematics and computer science, such as configuration spaces, homology computation, denoising, mesh compression, and topological data analysis.

In statistical mechanics, the eight-vertex model is a generalisation of the ice-type (six-vertex) models; it was discussed by Sutherland, and Fan & Wu, and solved by Baxter in the zero-field case.

A simplicial map is a function between two simplicial complexes, with the property that the images of the vertices of a simplex always span a simplex. Simplicial maps can be used to approximate continuous functions between topological spaces that can be triangulated; this is formalized by the simplicial approximation theorem.

In the geometry of numbers, the Klein polyhedron, named after Felix Klein, is used to generalize the concept of continued fractions to higher dimensions.

In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In Category theory and related fields of mathematics, an envelope is a construction that generalizes the operations of "exterior completion", like completion of a locally convex space, or Stone–Čech compactification of a topological space. A dual construction is called refinement.

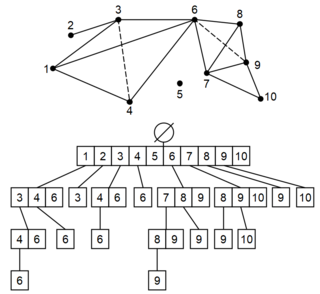
<span class="mw-page-title-main">Simplex tree</span> Topological data

In topological data analysis, a simplex tree is a type of trie used to represent efficiently any general simplicial complex. Through its nodes, this data structure notably explicitly represents all the simplices. Its flexible structure allows implementation of many basic operations useful to computing persistent homology. This data structure was invented by Jean-Daniel Boissonnat and Clément Maria in 2014, in the article The Simplex Tree: An Efficient Data Structure for General Simplicial Complexes. This data structure offers efficient operations on sparse simplicial complexes. For dense or maximal simplices, Skeleton-Blocker representations or Toplex Map representations are used.

References

1 2 3 Bryant, John L. (2001-01-01), Daverman, R. J.; Sher, R. B. (eds.), "Chapter 5 - Piecewise Linear Topology", Handbook of Geometric Topology, Amsterdam: North-Holland, pp. 219–259, ISBN 978-0-444-82432-5 , retrieved 2022-11-15
1 2 C. P. Rourke and B. J. Sanderson (1972). Introduction to Piecewise-Linear Topology. doi:10.1007/978-3-642-81735-9. ISBN 978-3-540-11102-3.
↑ Bridson, Martin; Haefliger, André (1999), Metric spaces of non-positive curvature, Springer, ISBN 3-540-64324-9

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 3 Bryant, John L. (2001-01-01), Daverman, R. J.; Sher, R. B. (eds.), "Chapter 5 - Piecewise Linear Topology", Handbook of Geometric Topology, Amsterdam: North-Holland, pp. 219–259, ISBN 978-0-444-82432-5 , retrieved 2022-11-15

[:1-2] 1 2 C. P. Rourke and B. J. Sanderson (1972). Introduction to Piecewise-Linear Topology. doi:10.1007/978-3-642-81735-9. ISBN 978-3-540-11102-3.

[3] Bridson, Martin; Haefliger, André (1999), Metric spaces of non-positive curvature, Springer, ISBN 3-540-64324-9

[1]

[2]

[3]