Related Research Articles

In graph theory, an isomorphism of graphsG and H is a bijection between the vertex sets of G and H

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
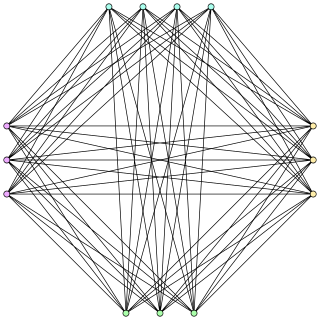
Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. Results in extremal graph theory deal with quantitative connections between various graph properties, both global and local, and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.
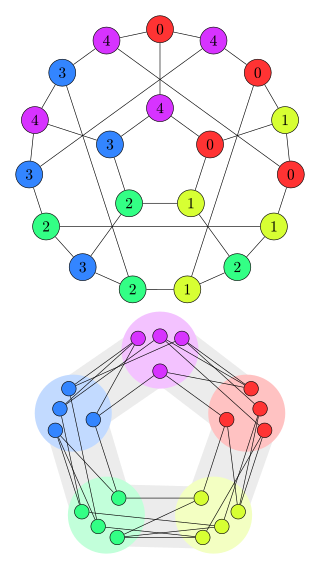
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

In graph theory, a complete coloring is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic numberψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.

In graph theory, a subcoloring is an assignment of colors to a graph's vertices such that each color class induces a vertex disjoint union of cliques. That is, each color class should form a cluster graph.

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

Jaroslav (Jarik) Nešetřil is a Czech mathematician, working at Charles University in Prague. His research areas include combinatorics, graph theory, algebra, posets, computer science.
In the mathematical field of graph theory, a core is a notion that describes behavior of a graph with respect to graph homomorphisms.

In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect.

In the mathematical field of graph theory, a star coloring of a graph G is a (proper) vertex coloring in which every path on four vertices uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected components that are star graphs. Star coloring has been introduced by Grünbaum (1973). The star chromatic number of G is the fewest colors needed to star color G.
Robin Thomas was a mathematician working in graph theory at the Georgia Institute of Technology.

In the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors. According to the four-color theorem, every graph that can be drawn in the plane without edge crossings can have its vertices colored using at most four different colors, so that the two endpoints of every edge have different colors, but according to Grötzsch's theorem only three colors are needed for planar graphs that do not contain three mutually adjacent vertices.
In graph theory, the tree-depth of a connected undirected graph is a numerical invariant of , the minimum height of a Trémaux tree for a supergraph of . This invariant and its close relatives have gone under many different names in the literature, including vertex ranking number, ordered chromatic number, and minimum elimination tree height; it is also closely related to the cycle rank of directed graphs and the star height of regular languages. Intuitively, where the treewidth of a graph measures how far it is from being a tree, this parameter measures how far a graph is from being a star.
In mathematics, in the areas of order theory and combinatorics, Mirsky's theorem characterizes the height of any finite partially ordered set in terms of a partition of the order into a minimum number of antichains. It is named for Leon Mirsky and is closely related to Dilworth's theorem on the widths of partial orders, to the perfection of comparability graphs, to the Gallai–Hasse–Roy–Vitaver theorem relating longest paths and colorings in graphs, and to the Erdős–Szekeres theorem on monotonic subsequences.
Gert Sabidussi was an Austrian mathematician specializing in combinatorics and graph theory.
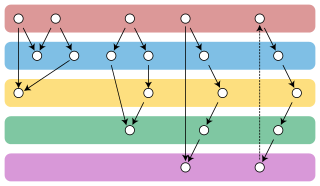
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph equals one plus the length of a longest path in an orientation of chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.
References
- ↑ Hell, Pavol; Nešetřil, Jaroslav (2004). Graphs and homomorphisms (Repr. ed.). Oxford: Oxford University Press. ISBN 978-0-19-852817-3.
- ↑ Hell, P.; Nešetřil, J. (1990). "On the complexity of H-coloring". J. Comb. Theory B. 48 (1): 92–110. doi:10.1016/0095-8956(90)90132-J.
- ↑ Graham, R.L.; Hell, P. (1985). "On the history of the minimum spanning tree problem". Annals of the History of Computing. 7 (1): 43–57. doi:10.1109/MAHC.1985.10011. S2CID 10555375.
- ↑ Hell, P.; Kirkpatrick, D.G. (1978). "Proceedings of the tenth annual ACM symposium on Theory of computing - STOC '78". STOC. pp. 240–245. doi: 10.1145/800133.804353 .
- ↑ Feder, T.; Hell, P.; Huang, Jing (1999). "List homomorphisms and circular arc graphs". Combinatorica. 19 (4): 487–505. CiteSeerX 10.1.1.22.5758 . doi:10.1007/s004939970003. S2CID 8316302.
- ↑ Fellow of the Society for Industrial and Applied Mathematics (SIAM) in 2012