Strong perfect graph theorem

Last updated

In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes (odd-length induced cycles of length at least 5) nor odd antiholes (complements of odd holes). It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 [1] and published by them in 2006.

Contents

The proof of the strong perfect graph theorem won for its authors a $10,000 prize offered by Gérard Cornuéjols of Carnegie Mellon University [2] and the 2009 Fulkerson Prize. [3]

Statement

A perfect graph is a graph in which, for every induced subgraph, the size of the maximum clique equals the minimum number of colors in a coloring of the graph; perfect graphs include many well-known graph classes including the bipartite graphs, chordal graphs, and comparability graphs. In his 1961 and 1963 works defining for the first time this class of graphs, Claude Berge observed that it is impossible for a perfect graph to contain an odd hole, an induced subgraph in the form of an odd-length cycle graph of length five or more, because odd holes have clique number two and chromatic number three. Similarly, he observed that perfect graphs cannot contain odd antiholes, induced subgraphs complementary to odd holes: an odd antihole with 2k + 1 vertices has clique number k and chromatic number k + 1, which is again impossible for perfect graphs. The graphs having neither odd holes nor odd antiholes became known as the Berge graphs.

Berge conjectured that every Berge graph is perfect, or equivalently that the perfect graphs and the Berge graphs define the same class of graphs. This became known as the strong perfect graph conjecture, until its proof in 2002, when it was renamed the strong perfect graph theorem.

Relation to the weak perfect graph theorem

Another conjecture of Berge, proved in 1972 by László Lovász, is that the complement of every perfect graph is also perfect. This became known as the perfect graph theorem, or (to distinguish it from the strong perfect graph conjecture/theorem) the weak perfect graph theorem. Because Berge's forbidden graph characterization is self-complementary, the weak perfect graph theorem follows immediately from the strong perfect graph theorem.

Proof ideas

The proof of the strong perfect graph theorem by Chudnovsky et al. follows an outline conjectured in 2001 by Conforti, Cornuéjols, Robertson, Seymour, and Thomas, according to which every Berge graph either forms one of five types of basic building block (special classes of perfect graphs) or it has one of four different types of structural decomposition into simpler graphs. A minimally imperfect Berge graph cannot have any of these decompositions, from which it follows that no counterexample to the theorem can exist. [4] This idea was based on previous conjectured structural decompositions of similar type that would have implied the strong perfect graph conjecture but turned out to be false. [5]

The five basic classes of perfect graphs that form the base case of this structural decomposition are the bipartite graphs, line graphs of bipartite graphs, complementary graphs of bipartite graphs, complements of line graphs of bipartite graphs, and double split graphs. It is easy to see that bipartite graphs are perfect: in any nontrivial induced subgraph, the clique number and chromatic number are both two and therefore are equal. The perfection of complements of bipartite graphs, and of complements of line graphs of bipartite graphs, are both equivalent to Kőnig's theorem relating the sizes of maximum matchings, maximum independent sets, and minimum vertex covers in bipartite graphs. The perfection of line graphs of bipartite graphs can be stated equivalently as the fact that bipartite graphs have chromatic index equal to their maximum degree, proven by Kőnig (1916). Thus, all four of these basic classes are perfect. The double split graphs are a relative of the split graphs that can also be shown to be perfect. [6]

The four types of decompositions considered in this proof are 2-joins, complements of 2-joins, balanced skew partitions, and homogeneous pairs.

A 2-join is a partition of the vertices of a graph into two subsets, with the property that the edges spanning the cut between these two subsets form two vertex-disjoint complete bipartite graphs. When a graph has a 2-join, it may be decomposed into induced subgraphs called "blocks", by replacing one of the two subsets of vertices by a shortest path within that subset that connects one of the two complete bipartite graphs to the other; when no such path exists, the block is formed instead by replacing one of the two subsets of vertices by two vertices, one for each complete bipartite subgraph. A 2-join is perfect if and only if its two blocks are both perfect. Therefore, if a minimally imperfect graph has a 2-join, it must equal one of its blocks, from which it follows that it must be an odd cycle and not Berge. For the same reason, a minimally imperfect graph whose complement has a 2-join cannot be Berge. [7]

A skew partition is a partition of a graph's vertices into two subsets, one of which induces a disconnected subgraph and the other of which has a disconnected complement; Chvátal (1985) had conjectured that no minimal counterexample to the strong perfect graph conjecture could have a skew partition. Chudnovsky et al. introduced some technical constraints on skew partitions, and were able to show that Chvátal's conjecture is true for the resulting "balanced skew partitions". The full conjecture is a corollary of the strong perfect graph theorem. [8]

A homogeneous pair is related to a modular decomposition of a graph. It is a partition of the graph into three subsets V1, V2, and V3 such that V1 and V2 together contain at least three vertices, V3 contains at least two vertices, and for each vertex v in V3 and each i in {1,2} either v is adjacent to all vertices in Vi or to none of them. It is not possible for a minimally imperfect graph to have a homogeneous pair. [9] Subsequent to the proof of the strong perfect graph conjecture, Chudnovsky (2006) simplified it by showing that homogeneous pairs could be eliminated from the set of decompositions used in the proof.

The proof that every Berge graph falls into one of the five basic classes or has one of the four types of decomposition follows a case analysis, according to whether certain configurations exist within the graph: a "stretcher", a subgraph that can be decomposed into three induced paths subject to certain additional constraints, the complement of a stretcher, and a "proper wheel", a configuration related to a wheel graph, consisting of an induced cycle together with a hub vertex adjacent to at least three cycle vertices and obeying several additional constraints. For each possible choice of whether a stretcher or its complement or a proper wheel exists within the given Berge graph, the graph can be shown to be in one of the basic classes or to be decomposable. [10] This case analysis completes the proof.

Notes

  1. ↑ Mackenzie (2002); Cornuéjols (2002).
  2. ↑ Mackenzie (2002).
  3. ↑ "2009 Fulkerson Prizes" (PDF), Notices of the American Mathematical Society: 1475–1476, December 2011.
  4. ↑ Cornuéjols (2002), Conjecture 5.1.
  5. ↑ Reed (1986); Hougardy (1991); Rusu (1997); Roussel, Rusu & Thuillier (2009), section 4.6 "The first conjectures".
  6. ↑ Roussel, Rusu & Thuillier (2009), Definition 4.39.
  7. ↑ Cornuéjols & Cunningham (1985); Cornuéjols (2002), Theorem 3.2 and Corollary 3.3.
  8. ↑ Seymour (2006); Roussel, Rusu & Thuillier (2009), section 4.7 "The skew partition"; Cornuéjols (2002), Theorems 4.1 and 4.2.
  9. ↑ Chvátal & Sbihi (1987); Cornuéjols (2002), Theorem 4.10.
  10. ↑ Cornuéjols (2002), Theorems 5.4, 5.5, and 5.6; Roussel, Rusu & Thuillier (2009), Theorem 4.42.

Related Research Articles

<span class="mw-page-title-main">Bipartite graph</span> Graph divided into two independent sets

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

<span class="mw-page-title-main">Perfect graph theorem</span> An undirected graph is perfect if and only if its complement graph is also perfect

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.

In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

<span class="mw-page-title-main">Edge coloring</span> Problem of coloring a graphs edges such that meeting edges do not match

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

<span class="mw-page-title-main">Meyniel graph</span> Graph where all odd cycles of length ≥ 5 has 2+ chords

In graph theory, a Meyniel graph is a graph in which every odd cycle of length five or more has at least two chords. The chords may be uncrossed or they may cross each other, as long as there are at least two of them.

In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem states that, in any finite partially ordered set, the maximum size of an antichain of incomparable elements equals the minimum number of chains needed to cover all elements. This number is called the width of the partial order. The theorem is named for the mathematician Robert P. Dilworth, who published it in 1950.

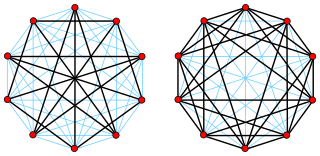
<span class="mw-page-title-main">Complement graph</span> Graph with same nodes but opposite connections as another

In the mathematical field of graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two distinct vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

<span class="mw-page-title-main">Paul Seymour (mathematician)</span> British mathematician

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges, from the original graph, connecting pairs of vertices in that subset.

<span class="mw-page-title-main">Graph factorization</span>

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

<span class="mw-page-title-main">Factor-critical graph</span> Graph of n vertices with a perfect matching for every subgraph of n-1 vertices

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every induced subgraph of n − 1 vertices has a perfect matching.

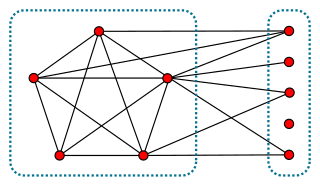
<span class="mw-page-title-main">Split graph</span> Graph which partitions into a clique and independent set

In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak, where they called these graphs "polar graphs".

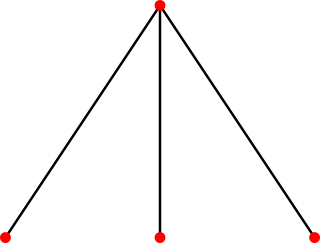
<span class="mw-page-title-main">Claw-free graph</span> Graph without four-vertex star subgraphs

In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

<span class="mw-page-title-main">Distance-hereditary graph</span> Graph whose induced subgraphs preserve distance

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

<span class="mw-page-title-main">Maria Chudnovsky</span> Mathematician and engineer

Maria Chudnovsky is an Israeli-American mathematician working on graph theory and combinatorial optimization. She is a 2012 MacArthur Fellow.

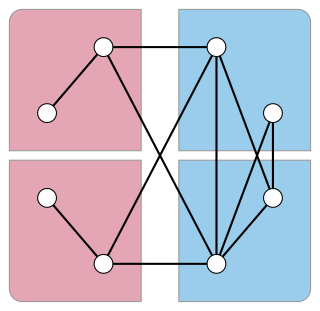
<span class="mw-page-title-main">Skew partition</span>

In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

<span class="mw-page-title-main">Petersen's theorem</span>

In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:

Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.

In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.