Split graph

Last updated December 13, 2023 • 6 min readFrom Wikipedia, The Free Encyclopedia

In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földesand Hammer ( 1977a , 1977b ), and independently introduced by Tyshkevich andChernyak ( 1979 ), where they called these graphs "polar graphs" (Russian : полярные графы).^[1]

Relation to other graph families

From the definition, split graphs are clearly closed under complementation.^[3] Another characterization of split graphs involves complementation: they are chordal graphs the complements of which are also chordal.^[4] Just as chordal graphs are the intersection graphs of subtrees of trees, split graphs are the intersection graphs of distinct substars of star graphs.^[5] Almost all chordal graphs are split graphs; that is, in the limit as n goes to infinity, the fraction of n-vertex chordal graphs that are split approaches one.^[6]

Because chordal graphs are perfect, so are the split graphs. The double split graphs, a family of graphs derived from split graphs by doubling every vertex (so the clique comes to induce an antimatching and the independent set comes to induce a matching), figure prominently as one of five basic classes of perfect graphs from which all others can be formed in the proof by Chudnovsky et al. (2006) of the Strong Perfect Graph Theorem.

If a graph is both a split graph and an interval graph, then its complement is both a split graph and a comparability graph, and vice versa. The split comparability graphs, and therefore also the split interval graphs, can be characterized in terms of a set of three forbidden induced subgraphs.^[7] The split cographs are exactly the threshold graphs. The split permutation graphs are exactly the interval graphs that have interval graph complements;^[8] these are the permutation graphs of skew-merged permutations.^[9] Split graphs have cochromatic number 2.

Algorithmic problems

Let $G$ be a split graph, partitioned into a clique $C$ and an independent set $i$ . Then every maximal clique in a split graph is either $C$ itself, or the neighborhood of a vertex in $i$ . Thus, it is easy to identify the maximum clique, and complementarily the maximum independent set in a split graph. In any split graph, one of the following three possibilities must be true:^[10]

There exists a vertex $x$ in $i$ such that $C \cup {x}$ is complete. In this case, $C \cup {x}$ is a maximum clique and $i$ is a maximum independent set.
There exists a vertex $x$ in $C$ such that $i \cup {x}$ is independent. In this case, $i \cup {x}$ is a maximum independent set and $C$ is a maximum clique.
$C$ is a maximal clique and $i$ is a maximal independent set. In this case, $G$ has a unique partition $(C, i)$ into a clique and an independent set, $C$ is the maximum clique, and $i$ is the maximum independent set.

Some other optimization problems that are NP-complete on more general graph families, including graph coloring, are similarly straightforward on split graphs. Finding a Hamiltonian cycle remains NP-complete even for split graphs which are strongly chordal graphs.^[11] It is also well known that the Minimum Dominating Set problem remains NP-complete for split graphs.^[12]

Degree sequences

One remarkable property of split graphs is that they can be recognized solely from their degree sequences. Let the degree sequence of a graph $G$ be $d 1 \geq d 2 \geq \dots \geq d n$ , and let $m$ be the largest value of $i$ such that $d i \geq i - 1$ . Then $G$ is a split graph if and only if

\sum _{i=1}^{m}d_{i}=m(m-1)+\sum _{i=m+1}^{n}d_{i}.

If this is the case, then the $m$ vertices with the largest degrees form a maximum clique in $G$ , and the remaining vertices constitute an independent set.^[13]

The splittance of an arbitrary graph measures the extent to which this inequality fails to be true. If a graph is not a split graph, then the smallest sequence of edge insertions and removals that make it into a split graph can be obtained by adding all missing edges between the $m$ vertices with the largest degrees, and removing all edges between pairs of the remaining vertices; the splittance counts the number of operations in this sequence.^[14]

Counting split graphs

Royle (2000) showed that (unlabeled) n-vertex split graphs are in one-to-one correspondence with certain Sperner families. Using this fact, he determined a formula for the number of nonisomorphic split graphs on n vertices. For small values of n, starting from n = 1, these numbers are

1, 2, 4, 9, 21, 56, 164, 557, 2223, 10766, 64956, 501696, ... (sequence A048194 in the OEIS ).

This enumerative result was also proved earlier by Tyshkevich & Chernyak (1990).

Notes

↑ Földes & Hammer (1977a) had a more general definition, in which the graphs they called split graphs also included bipartite graphs (that is, graphs that be partitioned into two independent sets) and the complements of bipartite graphs (that is, graphs that can be partitioned into two cliques). Földes & Hammer (1977b) use the definition given here, which has been followed in the subsequent literature; for instance, it is Brandstädt, Le & Spinrad (1999), Definition 3.2.3, p.41.
↑ Földes & Hammer (1977a); Golumbic (1980), Theorem 6.3, p. 151.
↑ Golumbic (1980), Theorem 6.1, p. 150.
↑ Földes & Hammer (1977a); Golumbic (1980), Theorem 6.3, p. 151; Brandstädt, Le & Spinrad (1999), Theorem 3.2.3, p. 41.
↑ McMorris & Shier (1983); Voss (1985); Brandstädt, Le & Spinrad (1999), Theorem 4.4.2, p. 52.
↑ Bender, Richmond & Wormald (1985).
↑ Földes & Hammer (1977b); Golumbic (1980), Theorem 9.7, page 212.
↑ Brandstädt, Le & Spinrad (1999), Corollary 7.1.1, p. 106, and Theorem 7.1.2, p. 107.
↑ Kézdy, Snevily & Wang (1996).
↑ Hammer & Simeone (1981); Golumbic (1980), Theorem 6.2, p. 150.
↑ Müller (1996)
↑ Bertossi (1984)
↑ Hammer & Simeone (1981); Tyshkevich (1980); Tyshkevich, Melnikow & Kotov (1981); Golumbic (1980), Theorem 6.7 and Corollary 6.8, p. 154; Brandstädt, Le & Spinrad (1999), Theorem 13.3.2, p. 203. Merris (2003) further investigates the degree sequences of split graphs.
↑ Hammer & Simeone (1981).

Related Research Articles

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets $and, that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.$

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

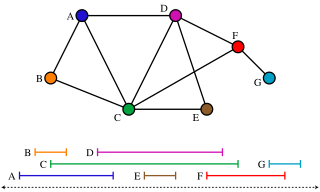
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph $is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.$

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.

In the mathematical discipline of graph theory, the line graph of an undirected graph $G$ is another graph $L(G)$ that represents the adjacencies between edges of $G$ . $L(G)$ is constructed in the following way: for each edge in $G$ , make a vertex in $L(G)$ ; for every two edges in $G$ that have a vertex in common, make an edge between their corresponding vertices in $L(G)$ .

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

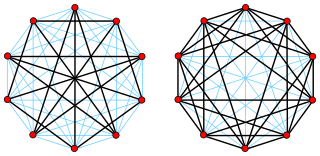
In the mathematical field of graph theory, the complement or inverse of a graph $G$ is a graph $H$ on the same vertices such that two distinct vertices of $H$ are adjacent if and only if they are not adjacent in $G$ . That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order. Comparability graphs have also been called transitively orientable graphs, partially orderable graphs, containment graphs, and divisor graphs. An incomparability graph is an undirected graph that connects pairs of elements that are not comparable to each other in a partial order.

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $)$
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In the mathematical field of graph theory, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.

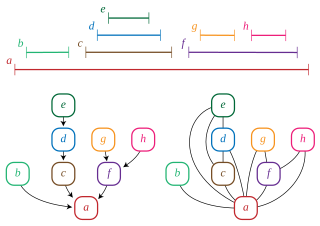
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.

In graph theory, a perfectly orderable graph is a graph whose vertices can be ordered in such a way that a greedy coloring algorithm with that ordering optimally colors every induced subgraph of the given graph. Perfectly orderable graphs form a special case of the perfect graphs, and they include the chordal graphs, comparability graphs, and distance-hereditary graphs. However, testing whether a graph is perfectly orderable is NP-complete.

In computer science, lexicographic breadth-first search or Lex-BFS is a linear time algorithm for ordering the vertices of a graph. The algorithm is different from a breadth-first search, but it produces an ordering that is consistent with breadth-first search.

In the mathematical area of graph theory, an undirected graph $G$ is strongly chordal if it is a chordal graph and every cycle of even length in $G$ has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.

In graph theory, the modular decomposition is a decomposition of a graph into subsets of vertices called modules. A module is a generalization of a connected component of a graph. Unlike connected components, however, one module can be a proper subset of another. Modules therefore lead to a recursive (hierarchical) decomposition of the graph, instead of just a partition.

In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.

References

Bender, E. A.; Richmond, L. B.; Wormald, N. C. (1985), "Almost all chordal graphs split", J. Austral. Math. Soc., A, 38 (2): 214–221, doi: 10.1017/S1446788700023077 , MR 0770128 .
Bertossi, Alan A. (1984), "Dominating sets for split and bipartite graphs", Information Processing Letters , 19: 37–40, doi:10.1016/0020-0190(84)90126-1 .
Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy (1999), Graph Classes: A Survey , SIAM Monographs on Discrete Mathematics and Applications, ISBN 0-89871-432-X .
Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem", Annals of Mathematics , 164 (1): 51–229, arXiv: math/0212070 , doi:10.4007/annals.2006.164.51, MR 2233847 .
Földes, Stéphane; Hammer, Peter Ladislaw (1977a), "Split graphs", Proceedings of the Eighth Southeastern Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1977), Congressus Numerantium, vol. XIX, Winnipeg: Utilitas Math., pp. 311–315, MR 0505860 .
Földes, Stéphane; Hammer, Peter Ladislaw (1977b), "Split graphs having Dilworth number two", Canadian Journal of Mathematics , 29 (3): 666–672, doi: 10.4153/CJM-1977-069-1 , MR 0463041 .
Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7, MR 0562306 .
Hammer, Peter Ladislaw; Simeone, Bruno (1981), "The splittance of a graph", Combinatorica , 1 (3): 275–284, doi:10.1007/BF02579333, MR 0637832 .
Kézdy, André E.; Snevily, Hunter S.; Wang, Chi (1996), "Partitioning permutations into increasing and decreasing subsequences", Journal of Combinatorial Theory, Series A, 73 (2): 353–359, doi: 10.1016/S0097-3165(96)80012-4 , MR 1370138 .
McMorris, F. R.; Shier, D. R. (1983), "Representing chordal graphs on K_1,n", Commentationes Mathematicae Universitatis Carolinae, 24: 489–494, MR 0730144 .
Merris, Russell (2003), "Split graphs", European Journal of Combinatorics , 24 (4): 413–430, doi: 10.1016/S0195-6698(03)00030-1 , MR 1975945 .
Müller, Haiko (1996), "Hamiltonian Circuits in Chordal Bipartite Graphs", Discrete Mathematics , 156: 291–298, doi: 10.1016/0012-365x(95)00057-4 .
Royle, Gordon F. (2000), "Counting set covers and split graphs" (PDF), Journal of Integer Sequences, 3 (2): 00.2.6, MR 1778996 .
Tyshkevich, Regina I. (1980), "[The canonical decomposition of a graph]", Doklady Akademii Nauk SSSR (in Russian), 24: 677–679, MR 0587712
Tyshkevich, Regina I.; Chernyak, A. A. (1979), "Canonical partition of a graph defined by the degrees of its vertices" Каноническое разложение графа, определяемого степенями его вершин (PDF), Isv. Akad. Nauk BSSR, Ser. Fiz.-Mat. Nauk (in Russian), 5: 14–26, MR 0554162 .
Tyshkevich, Regina I.; Chernyak, A. A. (1990), Еще один метод перечисления непомеченных комбинаторных объектов, Mat. Zametki (in Russian), 48 (6): 98–105, MR 1102626 . Translated as "Yet another method of enumerating unmarked combinatorial objects" (1990), Mathematical notes of the Academy of Sciences of the USSR48 (6): 1239–1245, doi:10.1007/BF01240267.
Tyshkevich, Regina I.; Melnikow, O. I.; Kotov, V. M. (1981), "On graphs and degree sequences: the canonical decomposition", Kibernetika (in Russian), 6: 5–8, MR 0689420 .
Voss, H.-J. (1985), "Note on a paper of McMorris and Shier", Commentationes Mathematicae Universitatis Carolinae, 26: 319–322, MR 0803929 .