Induced path

Last updated November 08, 2022

In the mathematical area of graph theory, an induced path in an undirected graph $G$ is a path that is an induced subgraph of $G$ . That is, it is a sequence of vertices in $G$ such that each two adjacent vertices in the sequence are connected by an edge in $G$ , and each two nonadjacent vertices in the sequence are not connected by any edge in $G$ . An induced path is sometimes called a snake, and the problem of finding long induced paths in hypercube graphs is known as the snake-in-the-box problem.

The length of the longest induced path in a graph has sometimes been called the detour number of the graph;^[1] for sparse graphs, having bounded detour number is equivalent to having bounded tree-depth.^[2] The induced path number of a graph $G$ is the smallest number of induced paths into which the vertices of the graph may be partitioned,^[3] and the closely related path cover number of $G$ is the smallest number of induced paths that together include all vertices of $G$ .^[4] The girth of a graph is the length of its shortest cycle, but this cycle must be an induced cycle as any chord could be used to produce a shorter cycle; for similar reasons the odd girth of a graph is also the length of its shortest odd induced cycle.

Example

The illustration shows a cube, a graph with eight vertices and twelve edges, and an induced path of length four in this graph. A straightforward case analysis shows that there can be no longer induced path in the cube, although it has an induced cycle of length six. The problem of finding the longest induced path or cycle in a hypercube, first posed by Kautz (1958), is known as the snake-in-the-box problem, and it has been studied extensively due to its applications in coding theory and engineering.

Characterization of graph families

Many important graph families can be characterized in terms of the induced paths or cycles of the graphs in the family.

Trivially, the connected graphs with no induced path of length two are the complete graphs, and the connected graphs with no induced cycle are the trees.
A triangle-free graph is a graph with no induced cycle of length three.
The cographs are exactly the graphs with no induced path of length three.
The chordal graphs are the graphs with no induced cycle of length four or more.
The even-hole-free graphs are the graphs containing no induced cycles with an even number of vertices.
The trivially perfect graphs are the graphs that have neither an induced path of length three nor an induced cycle of length four.
By the strong perfect graph theorem, the perfect graphs are the graphs with no odd hole and no odd antihole.
The distance-hereditary graphs are the graphs in which every induced path is a shortest path, and the graphs in which every two induced paths between the same two vertices have the same length.
The block graphs are the graphs in which there is at most one induced path between any two vertices, and the connected block graphs are the graphs in which there is exactly one induced path between every two vertices.

Algorithms and complexity

It is NP-complete to determine, for a graph G and parameter k, whether the graph has an induced path of length at least k. Garey & Johnson (1979) credit this result to an unpublished communication of Mihalis Yannakakis. However, this problem can be solved in polynomial time for certain graph families, such as asteroidal-triple-free graphs^[5] or graphs with no long holes.^[6]

It is also NP-complete to determine whether the vertices of a graph can be partitioned into two induced paths, or two induced cycles.^[7] As a consequence, determining the induced path number of a graph is NP-hard.

The complexity of approximating the longest induced path or cycle problems can be related to that of finding large independent sets in graphs, by the following reduction.^[8] From any graph G with n vertices, form another graph H with twice as many vertices as G, by adding to Gn(n − 1)/2 vertices having two neighbors each, one for each pair of vertices in G. Then if G has an independent set of size k, H must have an induced path and an induced cycle of length 2k, formed by alternating vertices of the independent set in G with vertices of I. Conversely, if H has an induced path or cycle of length k, any maximal set of nonadjacent vertices in G from this path or cycle forms an independent set in G of size at least k/3. Thus, the size of the maximum independent set in G is within a constant factor of the size of the longest induced path and the longest induced cycle in H. Therefore, by the results of Håstad (1996) on inapproximability of independent sets, unless NP=ZPP, there does not exist a polynomial time algorithm for approximating the longest induced path or the longest induced cycle to within a factor of O(n^1/2-ε) of the optimal solution.

Holes (and antiholes in graphs without chordless cycles of length 5) in a graph with n vertices and m edges may be detected in time (n+m²).^[9]

Atomic cycles

Atomic cycles are a generalization of chordless cycles, that contain no n-chords. Given some cycle, an n-chord is defined as a path of length n connecting two points on the cycle, where n is less than the length of the shortest path on the cycle connecting those points. If a cycle has no n-chords, it is called an atomic cycle, because it cannot be decomposed into smaller cycles.^[10] In the worst case, the atomic cycles in a graph can be enumerated in O(m²) time, where m is the number of edges in the graph.

Related Research Articles

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

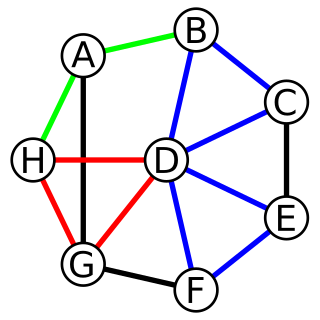
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.

<span class="mw-page-title-main">Hamiltonian path</span> Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph $is perfect if and only if for all we have .$

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes nor odd antiholes. It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 and published by them in 2006.

<span class="mw-page-title-main">Graph property</span> Property of graphs that depends only on abstract structure

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges connecting pairs of vertices in that subset.

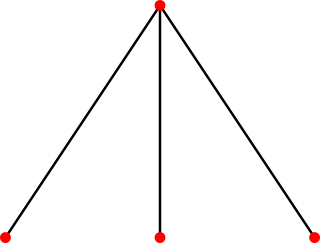
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of $vertices from an n -vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.$

In the mathematical area of graph theory, an undirected graph $G$ is strongly chordal if it is a chordal graph and every cycle of even length in $G$ has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.

In graph theory, the tree-depth of a connected undirected graph $is a numerical invariant of, the minimum height of a Trémaux tree for a supergraph of . This invariant and its close relatives have gone under many different names in the literature, including vertex ranking number, ordered chromatic number, and minimum elimination tree height; it is also closely related to the cycle rank of directed graphs and the star height of regular languages. Intuitively, where the treewidth of a graph measures how far it is from being a tree, this parameter measures how far a graph is from being a star.$

In graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.

In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.

In network theory, the Wiener connector is a means of maximizing efficiency in connecting specified "query vertices" in a network. Given a connected, undirected graph and a set of query vertices in a graph, the minimum Wiener connector is an induced subgraph that connects the query vertices and minimizes the sum of shortest path distances among all pairs of vertices in the subgraph. In combinatorial optimization, the minimum Wiener connector problem is the problem of finding the minimum Wiener connector. It can be thought of as a version of the classic Steiner tree problem, where instead of minimizing the size of the tree, the objective is to minimize the distances in the subgraph.

In graph theory, a parity graph is a graph in which every two induced paths between the same two vertices have the same parity: either both paths have odd length, or both have even length. This class of graphs was named and first studied by Burlet & Uhry (1984).

References

Barioli, Francesco; Fallat, Shaun; Hogben, Leslie (2004). "Computation of minimal rank and path cover number for certain graphs" (PDF). Linear Algebra and Its Applications . 392: 289–303. doi: 10.1016/j.laa.2004.06.019 .
Berman, Piotr; Schnitger, Georg (1992). "On the complexity of approximating the independent set problem". Information and Computation . 96 (1): 77–94. doi: 10.1016/0890-5401(92)90056-L .
Buckley, Fred; Harary, Frank (1988). "On longest induced paths in graphs". Chinese Quarterly Journal of Mathematics. 3 (3): 61–65.
Chartrand, Gary; McCanna, Joseph; Sherwani, Naveed; Hossain, Moazzem; Hashmi, Jahangir (1994). "The induced path number of bipartite graphs". Ars Combinatoria . 37: 191–208.
Garey, Michael R.; Johnson, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness . W. H. Freeman. p. 196.
Gashler, Michael; Martinez, Tony (2012). "Robust manifold learning with CycleCut" (PDF). Connection Science. 24 (1): 57–69. doi:10.1080/09540091.2012.664122.
Gavril, Fănică (2002). "Algorithms for maximum weight induced paths". Information Processing Letters . 81 (4): 203–208. doi:10.1016/S0020-0190(01)00222-8.
Håstad, Johan (1996). "Clique is hard to approximate within n^1−ε". Proceedings of the 37th Annual IEEE Symposium on Foundations of Computer Science. pp. 627–636. doi:10.1109/SFCS.1996.548522.
Kautz, William H. (June 1958). "Unit-distance error-checking codes". IRE Transactions on Electronic Computers . EC-7 (2): 179–180. doi:10.1109/TEC.1958.5222529. S2CID 26649532.
Kratsch, Dieter; Müller, Haiko; Todinca, Ioan (2003). "Feedback vertex set and longest induced path on AT-free graphs". Graph-theoretic concepts in computer science. Berlin: Lecture Notes in Computer Science, Vol. 2880, Springer-Verlag. pp. 309–321. doi:10.1007/b93953. Archived from the original on 2006-11-25.
Le, Hoàng-Oanh; Le, Van Bang; Müller, Haiko (2003). "Splitting a graph into disjoint induced paths or cycles" (PDF). Discrete Applied Mathematics . The Second International Colloquium "Journées de l'Informatique Messine", Metz, 2000. 131 (1): 199–212. doi: 10.1016/S0166-218X(02)00425-0 . Archived from the original (PDF) on 2016-03-03.
Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012). "Chapter 6. Bounded height trees and tree-depth". Sparsity: Graphs, Structures, and Algorithms. Algorithms and Combinatorics. Vol. 28. Heidelberg: Springer. pp. 115–144. doi:10.1007/978-3-642-27875-4. ISBN 978-3-642-27874-7. MR 2920058.
Nikolopoulos, Stavros D.; Palios, Leonidas (2004). "Hole and antihole detection in graphs". Proceedings of the 15th ACM-SIAM Symposium on Discrete Algorithms. pp. 850–859.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Buckley & Harary (1988).

[2] Nešetřil & Ossona de Mendez (2012), Proposition 6.4, p. 122.

[3] Chartrand et al. (1994).

[4] Barioli, Fallat & Hogben (2004).

[5] Kratsch, Müller & Todinca (2003).

[6] Gavril (2002).

[7] Le, Le & Müller (2003).

[8] Berman & Schnitger (1992).

[9] Nikolopoulos & Palios (2004).

[10] Gashler & Martinez (2012).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]