Related Research Articles

In physics and materials science, plasticity, also known as plastic deformation, is the ability of a solid material to undergo permanent deformation, a non-reversible change of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the material itself. In engineering, the transition from elastic behavior to plastic behavior is known as yielding.
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.

A beam is a structural element that primarily resists loads applied laterally to the beam's axis. Its mode of deflection is primarily by bending. The loads applied to the beam result in reaction forces at the beam's support points. The total effect of all the forces acting on the beam is to produce shear forces and bending moments within the beams, that in turn induce internal stresses, strains and deflections of the beam. Beams are characterized by their manner of support, profile, equilibrium conditions, length, and their material.

In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress in slender columns.
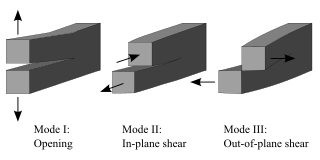
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.
In statics and structural mechanics, a structure is statically indeterminate when the static equilibrium equations – force and moment equilibrium conditions – are insufficient for determining the internal forces and reactions on that structure.
Fibre-reinforced plastic is a composite material made of a polymer matrix reinforced with fibres. The fibres are usually glass, carbon, aramid, or basalt. Rarely, other fibres such as paper, wood, or asbestos have been used. The polymer is usually an epoxy, vinyl ester, or polyester thermosetting plastic, though phenol formaldehyde resins are still in use.

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

Work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.
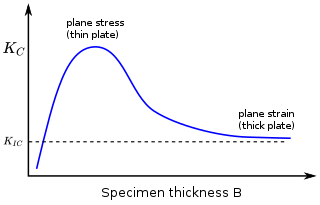
In materials science, fracture toughness is the critical stress intensity factor of a sharp crack where propagation of the crack suddenly becomes rapid and unlimited. A component's thickness affects the constraint conditions at the tip of a crack with thin components having plane stress conditions and thick components having plane strain conditions. Plane strain conditions give the lowest fracture toughness value which is a material property. The critical value of stress intensity factor in mode I loading measured under plane strain conditions is known as the plane strain fracture toughness, denoted . When a test fails to meet the thickness and other test requirements that are in place to ensure plane strain conditions, the fracture toughness value produced is given the designation . Fracture toughness is a quantitative way of expressing a material's resistance to crack propagation and standard values for a given material are generally available.
Specific modulus is a materials property consisting of the elastic modulus per mass density of a material. It is also known as the stiffness to weight ratio or specific stiffness. High specific modulus materials find wide application in aerospace applications where minimum structural weight is required. The dimensional analysis yields units of distance squared per time squared. The equation can be written as:

Plastic bending is a nonlinear behavior particular to members made of ductile materials that frequently achieve much greater ultimate bending strength than indicated by a linear elastic bending analysis. In both the plastic and elastic bending analyses of a straight beam, it is assumed that the strain distribution is linear about the neutral axis. In an elastic analysis this assumption leads to a linear stress distribution but in a plastic analysis the resulting stress distribution is nonlinear and is dependent on the beam’s material.

In the structural engineering beam theory, the term "plastic hinge" is used to describe the deformation of a section of a beam where plastic bending occurs. In earthquake engineering plastic hinge is also a type of energy damping device allowing plastic rotation [deformation] of an otherwise rigid column connection.

Honeycomb structures are natural or man-made structures that have the geometry of a honeycomb to allow the minimization of the amount of used material to reach minimal weight and minimal material cost. The geometry of honeycomb structures can vary widely but the common feature of all such structures is an array of hollow cells formed between thin vertical walls. The cells are often columnar and hexagonal in shape. A honeycomb shaped structure provides a material with minimal density and relative high out-of-plane compression properties and out-of-plane shear properties.

In engineering, an influence line graphs the variation of a function at a specific point on a beam or truss caused by a unit load placed at any point along the structure. Common functions studied with influence lines include reactions, shear, moment, and deflection (Deformation). Influence lines are important in designing beams and trusses used in bridges, crane rails, conveyor belts, floor girders, and other structures where loads will move along their span. The influence lines show where a load will create the maximum effect for any of the functions studied.
Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include area for tension and shear, radius of gyration for compression, and moment of inertia and polar moment of inertia for stiffness. Any relationship between these properties is highly dependent on the shape in question. Equations for the section moduli of common shapes are given below. There are two types of section moduli, the elastic section modulus and the plastic section modulus. The section moduli of different profiles can also be found as numerical values for common profiles in tables listing properties of such.
Structural engineering depends upon a detailed knowledge of loads, physics and materials to understand and predict how structures support and resist self-weight and imposed loads. To apply the knowledge successfully structural engineers will need a detailed knowledge of mathematics and of relevant empirical and theoretical design codes. They will also need to know about the corrosion resistance of the materials and structures, especially when those structures are exposed to the external environment.
The Müller-Breslau principle is a method to determine influence lines. The principle states that the influence lines of an action assumes the scaled form of the deflection displacement. OR, This principle states that "ordinate of ILD for a reactive force is given by ordinate of elastic curve if a unit deflection is applied in the direction of reactive force."
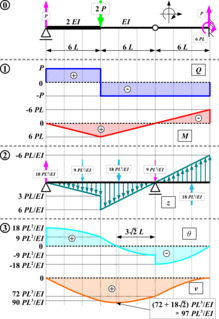
Conjugate beam is defined as the imaginary beam with the same dimensions (length) as that of the original beam but load at any point on the conjugate beam is equal to the bending moment at that point divided by EI. The conjugate-beam method is an engineering method to derive the slope and displacement of a beam. The conjugate-beam method was developed by H. Müller-Breslau in 1865. Essentially, it requires the same amount of computation as the moment-area theorems to determine a beam's slope or deflection; however, this method relies only on the principles of statics, so its application will be more familiar.
Materials that are used for biomedical or clinical applications are known as biomaterials. The following article deals with fifth generation biomaterials that are used for bone structure replacement. For any material to be classified for biomedical application three requirements must be met. The first requirement is that the material must be biocompatible; it means that the organism should not treat it as a foreign object. Secondly, the material should be biodegradable ; the material should harmlessly degrade or dissolve in the body of the organism to allow it to resume natural functioning. Thirdly, the material should be mechanically sound; for the replacement of load bearing structures, the material should possess equivalent or greater mechanical stability to ensure high reliability of the graft.