Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor.

Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, times, depths, or viewpoints. It is used in computer vision, medical imaging, military automatic target recognition, and compiling and analyzing images and data from satellites. Registration is necessary in order to be able to compare or integrate the data obtained from these different measurements.
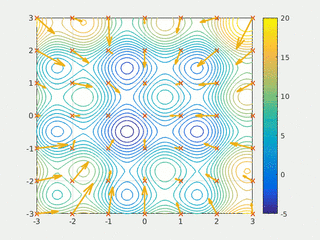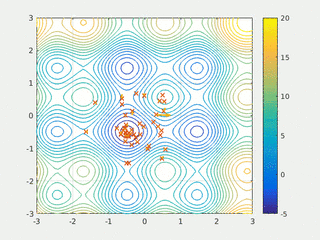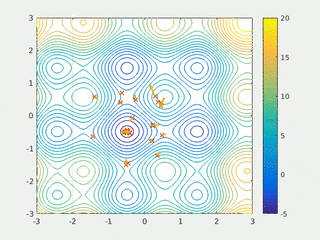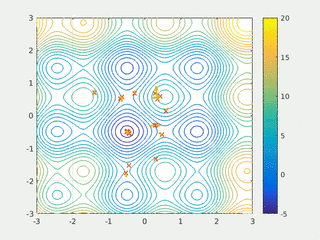
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
Random sample consensus (RANSAC) is an iterative method to estimate parameters of a mathematical model from a set of observed data that contains outliers, when outliers are to be accorded no influence on the values of the estimates. Therefore, it also can be interpreted as an outlier detection method. It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. The algorithm was first published by Fischler and Bolles at SRI International in 1981. They used RANSAC to solve the Location Determination Problem (LDP), where the goal is to determine the points in the space that project onto an image into a set of landmarks with known locations.
Model predictive control (MPC) is an advanced method of process control that is used to control a process while satisfying a set of constraints. It has been in use in the process industries in chemical plants and oil refineries since the 1980s. In recent years it has also been used in power system balancing models and in power electronics. Model predictive controllers rely on dynamic models of the process, most often linear empirical models obtained by system identification. The main advantage of MPC is the fact that it allows the current timeslot to be optimized, while keeping future timeslots in account. This is achieved by optimizing a finite time-horizon, but only implementing the current timeslot and then optimizing again, repeatedly, thus differing from a linear–quadratic regulator (LQR). Also MPC has the ability to anticipate future events and can take control actions accordingly. PID controllers do not have this predictive ability. MPC is nearly universally implemented as a digital control, although there is research into achieving faster response times with specially designed analog circuitry.
In control theory, a state observer or state estimator is a system that provides an estimate of the internal state of a given real system, from measurements of the input and output of the real system. It is typically computer-implemented, and provides the basis of many practical applications.
Adaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself to such changing conditions. Adaptive control is different from robust control in that it does not need a priori information about the bounds on these uncertain or time-varying parameters; robust control guarantees that if the changes are within given bounds the control law need not be changed, while adaptive control is concerned with control law changing itself.
Control reconfiguration is an active approach in control theory to achieve fault-tolerant control for dynamic systems. It is used when severe faults, such as actuator or sensor outages, cause a break-up of the control loop, which must be restructured to prevent failure at the system level. In addition to loop restructuring, the controller parameters must be adjusted to accommodate changed plant dynamics. Control reconfiguration is a building block toward increasing the dependability of systems under feedback control.
Electrical power system simulation involves power system modeling and network simulation in order to analyze electrical power systems using design/offline or real-time data. Power system simulation software's are a class of computer simulation programs that focus on the operation of electrical power systems. These types of computer programs are used in a wide range of planning and operational situations for electric power systems.
Visual servoing, also known as vision-based robot control and abbreviated VS, is a technique which uses feedback information extracted from a vision sensor to control the motion of a robot. One of the earliest papers that talks about visual servoing was from the SRI International Labs in 1979.
Miroslav Krstić is an American control theorist and Distinguished Professor of Mechanical and Aerospace Engineering at the University of California, San Diego (UCSD). Krstić is also the director of the Center for Control Systems and Dynamics at UCSD and a Senior Associate Vice Chancellor for Research. In the list of eminent researchers in systems and control, he is the youngest.

Dragoslav D. Šiljak is professor emeritus of Electrical Engineering at Santa Clara University, where he held the title of Benjamin and Mae Swig University Professor. He is best known for developing the mathematical theory and methods for control of complex dynamic systems characterized by large-scale, information structure constraints and uncertainty.
Adaptive collaborative control is the decision-making approach used in hybrid models consisting of finite-state machines with functional models as subcomponents to simulate behavior of systems formed through the partnerships of multiple agents for the execution of tasks and the development of work products. The term “collaborative control” originated from work developed in the late 1990s and early 2000 by Fong, Thorpe, and Baur (1999). It is important to note that according to Fong et al. in order for robots to function in collaborative control, they must be self-reliant, aware, and adaptive. In literature, the adjective “adaptive” is not always shown but is noted in the official sense as it is an important element of collaborative control. The adaptation of traditional applications of control theory in teleoperations sought initially to reduce the sovereignty of “humans as controllers/robots as tools” and had humans and robots working as peers, collaborating to perform tasks and to achieve common goals. Early implementations of adaptive collaborative control centered on vehicle teleoperation. Recent uses of adaptive collaborative control cover training, analysis, and engineering applications in teleoperations between humans and multiple robots, multiple robots collaborating among themselves, unmanned vehicle control, and fault tolerant controller design.
Active disturbance rejection control is a model-free control technique used for designing controllers for systems with unknown dynamics and external disturbances. This approach only necessitates an estimated representation of the system's behavior to design controllers that effectively counteract disturbances without causing any overshooting.

Wassim Michael Haddad is a Lebanese-Greek-American applied mathematician, scientist, and engineer, with research specialization in the areas of dynamical systems and control. His research has led to fundamental breakthroughs in applied mathematics, thermodynamics, stability theory, robust control, dynamical system theory, and neuroscience. Professor Haddad is a member of the faculty of the School of Aerospace Engineering at Georgia Institute of Technology, where he holds the rank of Professor and Chair of the Flight Mechanics and Control Discipline. Dr. Haddad is a member of the Academy of Nonlinear SciencesArchived 2016-03-04 at the Wayback Machine for recognition of paramount contributions to the fields of nonlinear stability theory, nonlinear dynamical systems, and nonlinear control and an IEEE Fellow for contributions to robust, nonlinear, and hybrid control systems.
The first smart antennas were developed for military communications and intelligence gathering. The growth of cellular telephone in the 1980s attracted interest in commercial applications. The upgrade to digital radio technology in the mobile phone, indoor wireless network, and satellite broadcasting industries created new opportunities for smart antennas in the 1990s, culminating in the development of the MIMO technology used in 4G wireless networks.
Ji-Feng Zhang was born in Shandong, China. He is currently the vice-chair of the technical board of the International Federation of Automatic Control (IFAC), the vice-president of the Systems Engineering Society of China (SESC), the vice-president of the Chinese Association of Automation (CAA), the chair of the technical committee on Control Theory (CAA), and the editor-in-chief for both All About Systems and Control and the Journal of Systems Science and Mathematical Sciences.
In regression analysis, an interval predictor model (IPM) is an approach to regression where bounds on the function to be approximated are obtained. This differs from other techniques in machine learning, where usually one wishes to estimate point values or an entire probability distribution. Interval Predictor Models are sometimes referred to as a nonparametric regression technique, because a potentially infinite set of functions are contained by the IPM, and no specific distribution is implied for the regressed variables.






