 | This article needs additional citations for verification .(July 2016) |
In microbiology, the multiplicity of infection or MOI is the ratio of agents (e.g. phage or more generally virus, bacteria) to infection targets (e.g. cell). For example, when referring to a group of cells inoculated with virus particles, the MOI is the ratio of the number of virus particles to the number of target cells present in a defined space. [1]
The actual number of viruses or bacteria that will enter any given cell is a stochastic process: some cells may absorb more than one infectious agent, while others may not absorb any. Before determining the multiplicity of infection, it's absolutely necessary to have a well-isolated agent, as crude agents may not produce reliable and reproducible results. The probability that a cell will absorb virus particles or bacteria when inoculated with an MOI of can be calculated for a given population using a Poisson distribution. This application of Poisson's distribution was applied and described by Ellis and Delbrück. [2]
where is the multiplicity of infection or MOI, is the number of infectious agents that enter the infection target, and is the probability that an infection target (a cell) will get infected by infectious agents.
In fact, the infectivity of the virus or bacteria in question will alter this relationship. One way around this is to use a functional definition of infectious particles rather than a strict count, such as a plaque forming unit for viruses. [3]
For example, when an MOI of 1 (1 infectious viral particle per cell) is used to infect a population of cells, the probability that a cell will not get infected is , and the probability that it be infected by a single particle is , by two particles is , by three particles is , and so on.
The average percentage of cells that will become infected as a result of inoculation with a given MOI can be obtained by realizing that it is simply . Hence, the average fraction of cells that will become infected following an inoculation with an MOI of is given by:
which is approximately equal to for small values of .
As the MOI increases, the percentages of cells infected with at least one viral particle () also increases. [4]
| MOI | % Infected |
|---|---|
| 0 | 0% |
| 0.1 | 9.5% |
| 0.25 | 22.1% |
| 0.5 | 39.3% |
| 1.0 | 63.2% |
| 2.0 | 86.5% |
| 3.0 | 95.0% |
| 4.0 | 98.2% |
| 5.0 | 99.3% |
Virology is the scientific study of biological viruses. It is a subfield of microbiology that focuses on their detection, structure, classification and evolution, their methods of infection and exploitation of host cells for reproduction, their interaction with host organism physiology and immunity, the diseases they cause, the techniques to isolate and culture them, and their use in research and therapy.
An infection is the invasion of tissues by pathogens, their multiplication, and the reaction of host tissues to the infectious agent and the toxins they produce. An infectious disease, also known as a transmissible disease or communicable disease, is an illness resulting from an infection.
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes occur. For example, we can define rolling a 6 on some dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success. In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution.
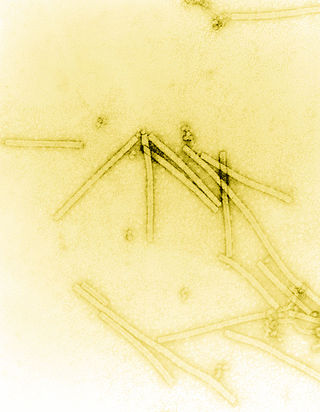
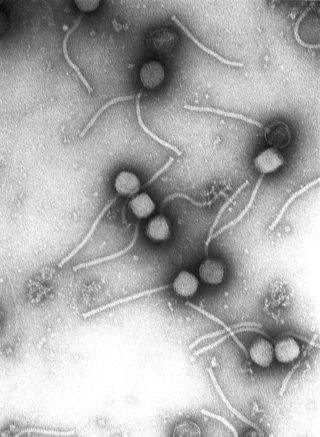
Tobacco mosaic virus (TMV) is a positive-sense single-stranded RNA virus species in the genus Tobamovirus that infects a wide range of plants, especially tobacco and other members of the family Solanaceae. The infection causes characteristic patterns, such as "mosaic"-like mottling and discoloration on the leaves. TMV was the first virus to be discovered. Although it was known from the late 19th century that a non-bacterial infectious disease was damaging tobacco crops, it was not until 1930 that the infectious agent was determined to be a virus. It is the first pathogen identified as a virus. The virus was crystallised by Wendell Meredith Stanley.
The vaccinia virus is a large, complex, enveloped virus belonging to the poxvirus family. It has a linear, double-stranded DNA genome approximately 190 kbp in length, which encodes approximately 250 genes. The dimensions of the virion are roughly 360 × 270 × 250 nm, with a mass of approximately 5–10 fg. The vaccinia virus is the source of the modern smallpox vaccine, which the World Health Organization (WHO) used to eradicate smallpox in a global vaccination campaign in 1958–1977. Although smallpox no longer exists in the wild, vaccinia virus is still studied widely by scientists as a tool for gene therapy and genetic engineering.
Viral evolution is a subfield of evolutionary biology and virology that is specifically concerned with the evolution of viruses. Viruses have short generation times, and many—in particular RNA viruses—have relatively high mutation rates. Although most viral mutations confer no benefit and often even prove deleterious to viruses, the rapid rate of viral mutation combined with natural selection allows viruses to quickly adapt to changes in their host environment. In addition, because viruses typically produce many copies in an infected host, mutated genes can be passed on to many offspring quickly. Although the chance of mutations and evolution can change depending on the type of virus, viruses overall have high chances for mutations.
Mathematical models can project how infectious diseases progress to show the likely outcome of an epidemic and help inform public health and plant health interventions. Models use basic assumptions or collected statistics along with mathematics to find parameters for various infectious diseases and use those parameters to calculate the effects of different interventions, like mass vaccination programs. The modelling can help decide which intervention(s) to avoid and which to trial, or can predict future growth patterns, etc.
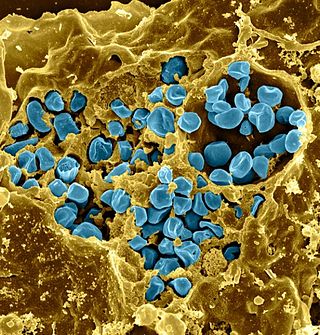
Francisella tularensis is a pathogenic species of Gram-negative coccobacillus, an aerobic bacterium. It is nonspore-forming, nonmotile, and the causative agent of tularemia, the pneumonic form of which is often lethal without treatment. It is a fastidious, facultative intracellular bacterium, which requires cysteine for growth. Due to its low infectious dose, ease of spread by aerosol, and high virulence, F. tularensis is classified as a Tier 1 Select Agent by the U.S. government, along with other potential agents of bioterrorism such as Yersinia pestis, Bacillus anthracis, and Ebola virus. When found in nature, Francisella tularensis can survive for several weeks at low temperatures in animal carcasses, soil, and water. In the laboratory, F. tularensis appears as small rods, and is grown best at 35–37 °C.
Plant viruses are viruses that have the potential to affect plants. Like all other viruses, plant viruses are obligate intracellular parasites that do not have the molecular machinery to replicate without a host. Plant viruses can be pathogenic to vascular plants.
The Luria–Delbrück experiment (1943) demonstrated that in bacteria, genetic mutations arise in the absence of selective pressure rather than being a response to it. Thus, it concluded Darwin's theory of natural selection acting on random mutations applies to bacteria as well as to more complex organisms. Max Delbrück and Salvador Luria won the 1969 Nobel Prize in Physiology or Medicine in part for this work.
Medical microbiology, the large subset of microbiology that is applied to medicine, is a branch of medical science concerned with the prevention, diagnosis and treatment of infectious diseases. In addition, this field of science studies various clinical applications of microbes for the improvement of health. There are four kinds of microorganisms that cause infectious disease: bacteria, fungi, parasites and viruses, and one type of infectious protein called prion.
A virus is a tiny infectious agent that reproduces inside the cells of living hosts. When infected, the host cell is forced to rapidly produce thousands of identical copies of the original virus. Unlike most living things, viruses do not have cells that divide; new viruses assemble in the infected host cell. But unlike simpler infectious agents like prions, they contain genes, which allow them to mutate and evolve. Over 4,800 species of viruses have been described in detail out of the millions in the environment. Their origin is unclear: some may have evolved from plasmids—pieces of DNA that can move between cells—while others may have evolved from bacteria.
The history of virology – the scientific study of viruses and the infections they cause – began in the closing years of the 19th century. Although Edward Jenner and Louis Pasteur developed the first vaccines to protect against viral infections, they did not know that viruses existed. The first evidence of the existence of viruses came from experiments with filters that had pores small enough to retain bacteria. In 1892, Dmitri Ivanovsky used one of these filters to show that sap from a diseased tobacco plant remained infectious to healthy tobacco plants despite having been filtered. Martinus Beijerinck called the filtered, infectious substance a "virus" and this discovery is considered to be the beginning of virology.
A virus is a submicroscopic infectious agent that replicates only inside the living cells of an organism. Viruses infect all life forms, from animals and plants to microorganisms, including bacteria and archaea. Viruses are found in almost every ecosystem on Earth and are the most numerous type of biological entity. Since Dmitri Ivanovsky's 1892 article describing a non-bacterial pathogen infecting tobacco plants and the discovery of the tobacco mosaic virus by Martinus Beijerinck in 1898, more than 11,000 of the millions of virus species have been described in detail. The study of viruses is known as virology, a subspeciality of microbiology.
A neutralizing antibody (NAb) is an antibody that defends a cell from a pathogen or infectious particle by neutralizing any effect it has biologically. Neutralization renders the particle no longer infectious or pathogenic. Neutralizing antibodies are part of the humoral response of the adaptive immune system against viruses, bacteria and microbial toxin. By binding specifically to surface structures (antigen) on an infectious particle, neutralizing antibodies prevent the particle from interacting with its host cells it might infect and destroy.
Virus quantification is counting or calculating the number of virus particles (virions) in a sample to determine the virus concentration. It is used in both research and development (R&D) in academic and commercial laboratories as well as in production situations where the quantity of virus at various steps is an important variable that must be monitored. For example, the production of virus-based vaccines, recombinant proteins using viral vectors, and viral antigens all require virus quantification to continually monitor and/or modify the process in order to optimize product quality and production yields and to respond to ever changing demands and applications. Other examples of specific instances where viruses need to be quantified include clone screening, multiplicity of infection (MOI) optimization, and adaptation of methods to cell culture.
The concept of a minimal infective dose (MID), also known as the infectious dose, has traditionally been used for infectious microorganisms that contaminate foods. MID was defined as the number of microorganisms ingested from which a pathology is observed in the consumer. For example, to cause gastrointestinal disorders, the food must contain more than 100,000 Salmonella per gram or 1000 per gram for salmonellosis. however, some viruses like DHBV( duck hepatitis B virus) need as low as 9.5 x 10(9) virus per milliliters to cause liver infections.To know the dose ingested, it is also necessary to know the mass of the portion. This may be calculated using the following formula:
In biology, a pathogen, in the oldest and broadest sense, is any organism or agent that can produce disease. A pathogen may also be referred to as an infectious agent, or simply a germ.
This glossary of virology is a list of definitions of terms and concepts used in virology, the study of viruses, particularly in the description of viruses and their actions. Related fields include microbiology, molecular biology, and genetics.
The Wells-Riley model is a simple model of the airborne transmission of infectious diseases, developed by William F. Wells and Richard L. Riley for tuberculosis and measles.
