
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

In mathematics, an n-sphere or a hypersphere is a topological space that is homeomorphic to a standardn-sphere, which is the set of points in (n + 1)-dimensional Euclidean space that are situated at a constant distance r from a fixed point, called the center. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit n-sphere or simply the n-sphere for brevity. In terms of the standard norm, the n-sphere is defined as

In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line, which may not intersect the generatrix. The surface created by this revolution and which bounds the solid is the surface of revolution.

A surface of revolution is a surface in Euclidean space created by rotating a curve one full revolution around an axis of rotation . The volume bounded by the surface created by this revolution is the solid of revolution.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory.

In mathematics, Pappus's centroid theorem is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.
The oceanic, wind driven Ekman spiral is the result of a force balance created by a shear stress force, Coriolis force and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the wind stress force. At the bottom of the ocean, the shear stress force is created by friction with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer Fridtjof Nansen during his Fram expedition. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer Vagn Walfrid Ekman, was the first person to physically explain this process.

In algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial
The second polar moment of area, also known as "polar moment of inertia" or even "moment of inertia", is a quantity used to describe resistance to torsional deformation (deflection), in objects with an invariant cross-section and no significant warping or out-of-plane deformation. It is a constituent of the second moment of area, linked through the perpendicular axis theorem. Where the planar second moment of area describes an object's resistance to deflection (bending) when subjected to a force applied to a plane parallel to the central axis, the polar second moment of area describes an object's resistance to deflection when subjected to a moment applied in a plane perpendicular to the object's central axis. Similar to planar second moment of area calculations, the polar second moment of area is often denoted as . While several engineering textbooks and academic publications also denote it as or , this designation should be given careful attention so that it does not become confused with the torsion constant, , used for non-cylindrical objects.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
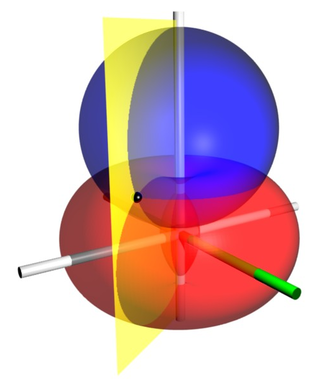
Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci. Thus, the two foci and in bipolar coordinates remain points in the bispherical coordinate system.
In physics, the Lemaître–Tolman metric, also known as the Lemaître–Tolman–Bondi metric or the Tolman metric, is a Lorentzian metric based on an exact solution of Einstein's field equations; it describes an isotropic and expanding universe which is not homogeneous, and is thus used in cosmology as an alternative to the standard Friedmann–Lemaître–Robertson–Walker metric to model the expansion of the universe. It has also been used to model a universe which has a fractal distribution of matter to explain the accelerating expansion of the universe. It was first found by Georges Lemaître in 1933 and Richard Tolman in 1934 and later investigated by Hermann Bondi in 1947.
The goat grazing problem is either of two related problems in recreational mathematics involving a tethered goat grazing a circular area: the interior grazing problem and the exterior grazing problem. The former involves grazing the interior of a circular area, and the latter, grazing an exterior of a circular area. For the exterior problem, the constraint that the rope can not enter the circular area dictates that the grazing area forms an involute. If the goat were instead tethered to a post on the edge of a circular path of pavement that did not obstruct the goat, the interior and exterior problem would be complements of a simple circular area.





























