In algebra, n-ary associativity is a generalization of the associative law to n-ary operations.
A ternary operation is ternary associative if one has always
that is, the operation gives the same result when any three adjacent elements are bracketed inside a sequence of five operands.
Similarly, an n-ary operation is n-ary associative if bracketing any n adjacent elements in a sequence of n + (n − 1) operands do not change the result. [1]
In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs.
In mathematics, a binary operation or dyadic operation is a rule for combining two elements to produce another element. More formally, a binary operation is an operation of arity two.
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible. Quasigroups differ from groups mainly in that the associative and identity element properties are optional.
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it.
In logic, mathematics, and computer science, arity is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank, but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree. In linguistics, it is usually named valency.
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A.
This is a list of operators in the C and C++ programming languages. All the operators listed exist in C++; the column "Included in C", states whether an operator is also present in C. Note that C does not support operator overloading.
In logic, a truth function is a function that accepts truth values as input and produces a unique truth value as output. In other words: the input and output of a truth function are all truth values; a truth function will always output exactly one truth value, and inputting the same truth value(s) will always output the same truth value. The typical example is in propositional logic, wherein a compound statement is constructed using individual statements connected by logical connectives; if the truth value of the compound statement is entirely determined by the truth value(s) of the constituent statement(s), the compound statement is called a truth function, and any logical connectives used are said to be truth functional.
In computer programming, the ternary conditional operator is a ternary operator that is part of the syntax for basic conditional expressions in several programming languages. It is commonly referred to as the conditional operator, ternary if, or inline if. An expression a ? b : c evaluates to b if the value of a is true, and otherwise to c. One can read it aloud as "if a then b otherwise c". The form a ? b : c is by far and large the most common, but alternative syntaxes do exist; for example, Raku uses the syntax a ?? b !! c to avoid confusion with the infix operators ? and !, whereas in Visual Basic .NET, it instead takes the form If(a, b, c).
In computer programming, operators are constructs defined within programming languages which behave generally like functions, but which differ syntactically or semantically.
In C and C++, a sequence point defines any point in a computer program's execution at which it is guaranteed that all side effects of previous evaluations will have been performed, and no side effects from subsequent evaluations have yet been performed. They are a core concept for determining the validity of and, if valid, the possible results of expressions. Adding more sequence points is sometimes necessary to make an expression defined and to ensure a single valid order of evaluation.
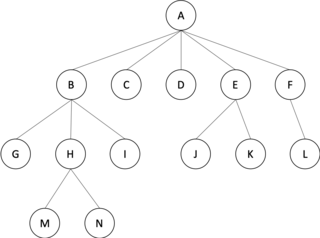
In graph theory, an m-ary tree is an arborescence in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.
In mathematics, an operation is a function which takes zero or more input values to a well-defined output value. The number of operands is the arity of the operation.
The conditional operator is supported in many programming languages. This term usually refers to ?: as in C, C++, C#, and JavaScript. However, in Java, this term can also refer to && and ||.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
In abstract algebra, a semiheap is an algebraic structure consisting of a non-empty set H with a ternary operation denoted that satisfies a modified associativity property:
In mathematics, and in particular universal algebra, the concept of an n-ary group is a generalization of the concept of a group to a set G with an n-ary operation instead of a binary operation. By an n-ary operation is meant any map f: Gn → G from the n-th Cartesian power of G to G. The axioms for an n-ary group are defined in such a way that they reduce to those of a group in the case n = 2. The earliest work on these structures was done in 1904 by Kasner and in 1928 by Dörnte; the first systematic account of polyadic groups was given in 1940 by Emil Leon Post in a famous 143-page paper in the Transactions of the American Mathematical Society.
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact.
Increment and decrement operators are unary operators that increase or decrease their operand by one.
 | This algebra-related article is a stub. You can help Wikipedia by expanding it. |
