Generalization

Last updated

A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. [1] Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation.

Contents

Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them.

However, the parts cannot be generalized into a whole—until a common relation is established among all parts. This does not mean that the parts are unrelated, only that no common relation has been established yet for the generalization.

The concept of generalization has broad application in many connected disciplines, and might sometimes have a more specific meaning in a specialized context (e.g. generalization in psychology, generalization in learning). [1]

In general, given two related concepts A and B,A is a "generalization" of B (equiv., B is a special case of A) if and only if both of the following hold:

For example, the concept animal is a generalization of the concept bird, since every bird is an animal, but not all animals are birds (dogs, for instance). For more, see Specialisation (biology).

Hypernym and hyponym

The connection of generalization to specialization (or particularization ) is reflected in the contrasting words hypernym and hyponym. A hypernym as a generic stands for a class or group of equally ranked items, such as the term tree which stands for equally ranked items such as peach and oak, and the term ship which stands for equally ranked items such as cruiser and steamer. In contrast, a hyponym is one of the items included in the generic, such as peach and oak which are included in tree, and cruiser and steamer which are included in ship. A hypernym is superordinate to a hyponym, and a hyponym is subordinate to a hypernym. [2]

Examples

Biological generalization

When the mind makes a generalization, it extracts the essence of a concept based on its analysis of similarities from many discrete objects. The resulting simplification enables higher-level thinking. Generalization process using trees.svg
When the mind makes a generalization, it extracts the essence of a concept based on its analysis of similarities from many discrete objects. The resulting simplification enables higher-level thinking.

An animal is a generalization of a mammal, a bird, a fish, an amphibian and a reptile.

Cartographic generalization of geo-spatial data

Generalization has a long history in cartography as an art of creating maps for different scale and purpose. Cartographic generalization is the process of selecting and representing information of a map in a way that adapts to the scale of the display medium of the map. In this way, every map has, to some extent, been generalized to match the criteria of display. This includes small cartographic scale maps, which cannot convey every detail of the real world. As a result, cartographers must decide and then adjust the content within their maps, to create a suitable and useful map that conveys the geospatial information within their representation of the world. [3]

Generalization is meant to be context-specific. That is to say, correctly generalized maps are those that emphasize the most important map elements, while still representing the world in the most faithful and recognizable way. The level of detail and importance in what is remaining on the map must outweigh the insignificance of items that were generalized—so as to preserve the distinguishing characteristics of what makes the map useful and important.

Mathematical generalizations

See also

Related Research Articles

<span class="mw-page-title-main">Cardinality</span> Definition of the number of elements in a set

In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.

<span class="mw-page-title-main">Map</span> Symbolic depiction of relationships

A map is a symbolic depiction emphasizing relationships between elements of some space, such as objects, regions, or themes.

<span class="mw-page-title-main">WordNet</span> Computational lexicon of English

WordNet is a lexical database of semantic relations between words that links words into semantic relations including synonyms, hyponyms, and meronyms. The synonyms are grouped into synsets with short definitions and usage examples. It can thus be seen as a combination and extension of a dictionary and thesaurus. While it is accessible to human users via a web browser, its primary use is in automatic text analysis and artificial intelligence applications. It was first created in the English language and the English WordNet database and software tools have been released under a BSD style license and are freely available for download from that WordNet website. There are now WordNets in more than 200 languages.

<span class="mw-page-title-main">Map projection</span> Systematic representation of the surface of a sphere or ellipsoid onto a plane

In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.

CycL in computer science and artificial intelligence is an ontology language used by Doug Lenat's Cyc artificial intelligence project. Ramanathan V. Guha was instrumental in the design of early versions of the language. There is a close variant of CycL known as MELD.

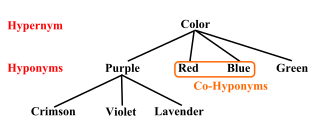
<span class="mw-page-title-main">Hypernymy and hyponymy</span> Semantic relations involving the type-of property

Hypernymy and hyponymy are the semantic relations between a generic term (hypernym) and a specific instance of it (hyponym). The hypernym is also called a supertype, umbrella term, or blanket term. The hyponym is a subtype of the hypernym. The semantic field of the hyponym is included within that of the hypernym. For example, pigeon, crow, and hen are all hyponyms of bird and animal; bird and animal are both hypernyms of pigeon, crow, and hen.

In database design, object-oriented programming and design, has-a is a composition relationship where one object "belongs to" another object, and behaves according to the rules of ownership. In simple words, has-a relationship in an object is called a member field of an object. Multiple has-a relationships will combine to form a possessive hierarchy.

In knowledge representation and ontology components, including for object-oriented programming and design, is-a is a subsumptive relationship between abstractions, wherein one class A is a subclass of another class B . In other words, type A is a subtype of type B when A's specification implies B's specification. That is, any object that satisfies A's specification also satisfies B's specification, because B's specification is weaker.

Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.

The fallacy of composition is an informal fallacy that arises when one infers that something is true of the whole from the fact that it is true of some part of the whole. A trivial example might be: "This tire is made of rubber; therefore, the vehicle of which it is a part is also made of rubber." This is fallacious, because vehicles are made with a variety of parts, most of which are not made of rubber. The fallacy of composition can apply even when a fact is true of every proper part of a greater entity, though. A more complicated example might be: "No atoms are alive. Therefore, nothing made of atoms is alive." This is a statement most people would consider incorrect, due to emergence, where the whole possesses properties not present in any of the parts.

In category theory, a branch of mathematics, a subobject is, roughly speaking, an object that sits inside another object in the same category. The notion is a generalization of concepts such as subsets from set theory, subgroups from group theory, and subspaces from topology. Since the detailed structure of objects is immaterial in category theory, the definition of subobject relies on a morphism that describes how one object sits inside another, rather than relying on the use of elements.

<span class="mw-page-title-main">Weak ordering</span> Mathematical ranking of a set

In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets and are in turn generalized by (strictly) partially ordered sets and preorders.

In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic. Interior algebras form a variety of modal algebras.

"Natural kind" is an intellectual grouping, or categorizing of things, in a manner that is reflective of the actual world and not just human interests. Some treat it as a classification identifying some structure of truth and reality that exists whether or not humans recognize it. Others treat it as intrinsically useful to the human mind, but not necessarily reflective of something more objective. Candidate examples of natural kinds are found in all the sciences, but the field of chemistry provides the paradigm example of elements.

Ontology learning is the automatic or semi-automatic creation of ontologies, including extracting the corresponding domain's terms and the relationships between the concepts that these terms represent from a corpus of natural language text, and encoding them with an ontology language for easy retrieval. As building ontologies manually is extremely labor-intensive and time-consuming, there is great motivation to automate the process.

A feature, in the context of geography and geographic information science, is something that exists at a moderate to global scale at a location in the space and scale of relevance to geography; that is, at or near the surface of Earth. It is an item of geographic information, and may be represented in maps, geographic information systems, remote sensing imagery, statistics, and other forms of geographic discourse. Such representations of features consist of descriptions of their inherent nature, their spatial form and location, and their characteristics or properties.

Cartographic generalization, or map generalization, includes all changes in a map that are made when one derives a smaller-scale map from a larger-scale map or map data. It is a core part of cartographic design. Whether done manually by a cartographer or by a computer or set of algorithms, generalization seeks to abstract spatial information at a high level of detail to information that can be rendered on a map at a lower level of detail.

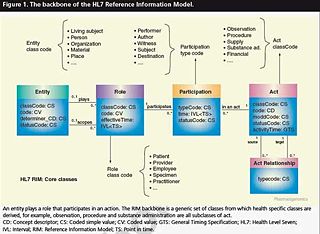
<span class="mw-page-title-main">Generic data model</span>

Generic data models are generalizations of conventional data models. They define standardised general relation types, together with the kinds of things that may be related by such a relation type.

In natural language processing, semantic compression is a process of compacting a lexicon used to build a textual document by reducing language heterogeneity, while maintaining text semantics. As a result, the same ideas can be represented using a smaller set of words.

<span class="mw-page-title-main">Taxonomy</span> Science of classification

Taxonomy is the practice and science of categorization or classification.

References

  1. 1 2 "Definition of generalization | Dictionary.com". www.dictionary.com. Retrieved 30 November 2019.
  2. ↑ Nordquist, Richard. "Definition and Examples of Hypernyms in English". ThoughtCo. Retrieved 30 November 2019.
  3. ↑ "Scale and Generalization". Axis Maps. 14 October 2019. Retrieved 30 November 2019.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.